题目内容
(本题满分12分)
在等差数列{an}中,若a2+a3+a4+a5=34,且a2·a5=52.求数列{an}的通项公式an.
在等差数列{an}中,若a2+a3+a4+a5=34,且a2·a5=52.求数列{an}的通项公式an.
(本题满分12分).
解:∵数列{an}是等差数列,∴a2+a3+a4+a5=2(a2+a5)=34,
∴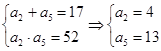 或
或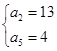 ,∴an=3n-2或an=-3n+19.
,∴an=3n-2或an=-3n+19.
解:∵数列{an}是等差数列,∴a2+a3+a4+a5=2(a2+a5)=34,
∴
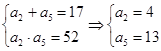 或
或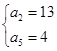 ,∴an=3n-2或an=-3n+19.
,∴an=3n-2或an=-3n+19.略

练习册系列答案
相关题目
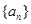 满足
满足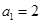 ,
,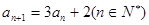 ,则该数列的通项公式
,则该数列的通项公式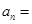
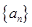 是公差大于0的等差数列,
是公差大于0的等差数列,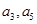 分别是方程
分别是方程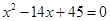 的两个实根
的两个实根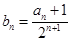 ,求数列
,求数列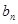 的前
的前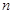 项和
项和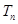
 的衰减来测定:在动植物的体内都含有微量的
的衰减来测定:在动植物的体内都含有微量的 ,则经过
,则经过 年后的残余量
年后的残余量 与
与 .
. 的值;
的值;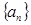 的通项为
的通项为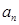 =
=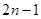 ,
,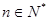 ,其前
,其前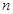 项和为
项和为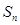 ,则使
,则使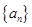 中,已知
中,已知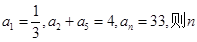 为( )
为( )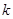 、
、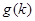 表示
表示
 例如
例如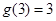 ,
,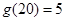 ,并且
,并且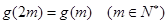 ,设
,设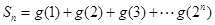
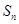 ;
;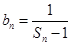 ,求证数列
,求证数列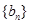 的前
的前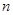 顶和
顶和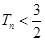 .
. }中,
}中,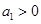 ,
,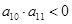 ,若此数列的前10项和
,若此数列的前10项和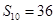 ,前18项和
,前18项和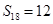 ,则数列{
,则数列{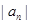 }的前18项和
}的前18项和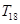 的值是( )
的值是( ) 的前n项和为Sn,且
的前n项和为Sn,且 则过点
则过点 的直线的斜率是______________
的直线的斜率是______________