题目内容
某地区的一种特色水果上市时间仅能持续几个月,预测上市初期和后期会因供不应求使价格呈连续上涨的态势,而中期又将出现供大于求使价格连续下跌,为准确研究其价格走势,下面给出的四个价格模拟函数中合适的是(其中p,q为常数,且q>1,x∈[0,5],x=0表示4月1日,x=1表示5月1日,…以此类推)
- A.f(x)=p•qx
- B.f(x)=px2+qx+1
- C.f(x)=x(x-q)2+p
- D.f(x)=plnx+qx2
C
分析:从三个函数的单调上考虑,分析答案中四个函数的单调性,并与已知要求进行比照,即可得到拟合效果最好的函数模型.
解答:因为A中,f(x)=pqx,是单调函数,不满足要求;
B中,f(x)=px2+qx+1,为二次函数,有一个单调递增区间和一个单调递减区间,不满足要求;
C中,f(x)=(x-1)(x-q)2+q时,f′(x)=3x2-(4q+2)+q2+2q,令f′(x)=0,得x=q,x=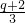 ,f(x)有两个零点,可以出现两个递增区间和一个递减区间,满足要求;
,f(x)有两个零点,可以出现两个递增区间和一个递减区间,满足要求;
D中,f(x)=plnx+qx2中,f′(x)= ,至多也只有一个单调递增区间和一个单调递减区间,不满足要求.
,至多也只有一个单调递增区间和一个单调递减区间,不满足要求.
故选C.
点评:本题主要考查函数模型的选择与应用,考查学生分析解决问题的能力,属于基础题.
分析:从三个函数的单调上考虑,分析答案中四个函数的单调性,并与已知要求进行比照,即可得到拟合效果最好的函数模型.
解答:因为A中,f(x)=pqx,是单调函数,不满足要求;
B中,f(x)=px2+qx+1,为二次函数,有一个单调递增区间和一个单调递减区间,不满足要求;
C中,f(x)=(x-1)(x-q)2+q时,f′(x)=3x2-(4q+2)+q2+2q,令f′(x)=0,得x=q,x=
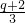 ,f(x)有两个零点,可以出现两个递增区间和一个递减区间,满足要求;
,f(x)有两个零点,可以出现两个递增区间和一个递减区间,满足要求;D中,f(x)=plnx+qx2中,f′(x)=
 ,至多也只有一个单调递增区间和一个单调递减区间,不满足要求.
,至多也只有一个单调递增区间和一个单调递减区间,不满足要求.故选C.
点评:本题主要考查函数模型的选择与应用,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某地区的一种特色水果上市时间仅能持续几个月,预测上市初期和后期会因供不应求使价格呈连续上涨的态势,而中期又将出现供大于求使价格连续下跌,为准确研究其价格走势,下面给出四个价格模拟函数中适合的是(其中为p、q常数,0<q<4,且x∈(0,5))( )
| A、f(x)=p•qx | B、f(x)=px2+qx+1 | C、f(x)=plnx+qx2 | D、f(x)=x(x-q)2+p |
 ;②
;② ;③
;③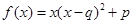 .(以上三式中
.(以上三式中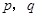 均为常数,且
均为常数,且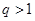 )
)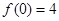 ,
,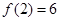 ,求出所选函数
,求出所选函数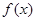 的解析式(注:函数的定义域是
的解析式(注:函数的定义域是 ).其中
).其中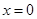 表示4月1日,
表示4月1日,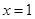 表示5月1日,…,依此类推;
表示5月1日,…,依此类推;