题目内容
某地区的一种特色水果上市时间仅能持续几个月，预测上市初期和后期会因供不应求使价格呈连续上涨的态势，而中期又将出现供大于求使价格连续下跌，为准确研究其价格走势，下面给出四个价格模拟函数中适合的是（其中为p、q常数，0＜q＜4，且x∈（0，5））（ ）
| A、f（x）=p•qx | B、f（x）=px2+qx+1 | C、f（x）=plnx+qx2 | D、f（x）=x（x-q）2+p |
分析：欲找出能较准确反映数学成绩与考试序次关系的模拟函数，主要依据是上市初期和后期会因供不应求使价格呈连续上涨的态势，而中期又将出现供大于求使价格连续下跌，故可从三个函数的单调上考虑，分析答案中四个函数的单调性，并与已知要求进行比照，即可得到拟合效果最好的函数模型．
解答：解：因为A中，f（x）=pqx，是单调函数，不满足要求；
B中，f（x）=px2+qx+1，为二次函数，有一个单调递增区间和一个单调递减区间，不满足要求；
C中，f（x）=plnx+qx2中，f′（x）=
+2qx，到多也只有一个单调递增区间和一个单调递减区间，不满足要求；
D中，f（x）=（x-1）（x-q）2+q时，f′（x）=3x2-（4q+2）+q2+2q，令f′（x）=0，得x=q，x=
，f（x）有两个零点，
可以出现两个递增区间和一个递减区间，满足要求．
故选D
B中，f（x）=px2+qx+1，为二次函数，有一个单调递增区间和一个单调递减区间，不满足要求；
C中，f（x）=plnx+qx2中，f′（x）=
| p |
| x |
D中，f（x）=（x-1）（x-q）2+q时，f′（x）=3x2-（4q+2）+q2+2q，令f′（x）=0，得x=q，x=
| q+2 |
| 3 |
可以出现两个递增区间和一个递减区间，满足要求．
故选D
点评：本小题主要考查函数模型的选择与应用，属于基础题．解决实际问题通常有四个步骤：（1）阅读理解，认真审题；（2）引进数学符号，建立数学模型；（3）利用数学的方法，得到数学结果；（4）转译成具体问题作出解答，其中关键是建立数学模型．
练习册系列答案
阅读快车系列答案
相关题目
；②
；③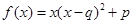
．（以上三式中
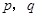均为常数，且
）
，
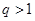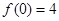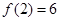，求出所选函数
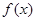的解析式（注：函数的定义域是
）．其中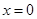
表示4月1日，
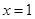表示5月1日，…，依此类推；