题目内容
在极坐标系中,已知圆 的圆心为
的圆心为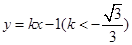 ,半径为
,半径为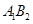 ,点
,点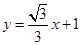 为圆
为圆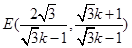 上异于极点
上异于极点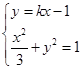 的动点,求弦
的动点,求弦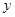 中点的轨迹的极坐标方程.
中点的轨迹的极坐标方程.
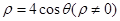 .
.
解析试题分析:求轨迹方程,第一步是设,求什么设什么,设弦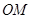 中点为
中点为 ,第二步找寻等量关系,因为点
,第二步找寻等量关系,因为点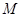 在圆
在圆 上,,圆
上,,圆 的极坐标方程为
的极坐标方程为 ,又
,又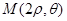 ,所以
,所以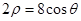 ,即
,即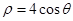 ,第三步去杂,又点
,第三步去杂,又点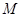 异于极点
异于极点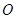 ,所以
,所以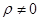 ,所以弦
,所以弦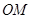 中点的轨迹的极坐标方程为
中点的轨迹的极坐标方程为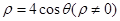 .
.
试题解析:由题意知,圆 的极坐标方程为
的极坐标方程为 , 4分
, 4分
设弦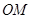 中点为
中点为 ,则
,则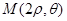 ,
,
因为点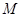 在圆
在圆 上,所以
上,所以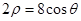 ,即
,即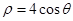 , 9分
, 9分
又点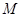 异于极点
异于极点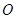 ,所以
,所以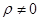 ,
,
所以弦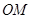 中点的轨迹的极坐标方程为
中点的轨迹的极坐标方程为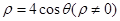 . 10分
. 10分
考点:轨迹方程

练习册系列答案
相关题目
 为极点,
为极点, 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点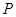 的直角坐标为
的直角坐标为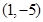 ,点
,点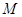 的极坐标为
的极坐标为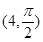 ,若直线
,若直线 过点
过点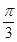 ,圆
,圆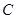 以
以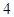 为半径.
为半径.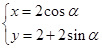 (
(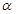 为参数)M是C1上的动点,P点满足
为参数)M是C1上的动点,P点满足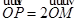 ,P点的轨迹为曲线C2
,P点的轨迹为曲线C2 与C1的异于极点的交点为A,与C2的异于极点的交点为B,求
与C1的异于极点的交点为A,与C2的异于极点的交点为B,求 .
.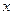 轴的正半轴为极轴,并在两种坐标系中取相同的长度单位。已知直线的极坐标方程为
轴的正半轴为极轴,并在两种坐标系中取相同的长度单位。已知直线的极坐标方程为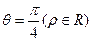 ,它与曲线
,它与曲线 (
( 为参数)相交于两点A和B,则|AB|=_______.
为参数)相交于两点A和B,则|AB|=_______.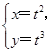 (t为参数)相交于A、B两点,求|AB|.
(t为参数)相交于A、B两点,求|AB|.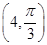 ,求|CP|.
,求|CP|.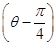 =2
=2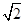 .
.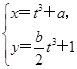 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.