题目内容
函数y=ax与y=ax2+bx（a＞0，a≠a，ab=2）在同一坐标系中的图象可能是
- A.
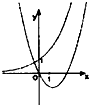
- B.
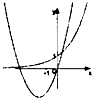
- C.
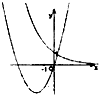
- D.
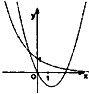
C
分析：利用指数函数的图象与性质及二次函数的图象与性质即可求得答案．
解答：对于A，∵a＞0，a≠b，ab=2，
∴b=
＞0，
∴y=ax2+bx的对称轴x=-
＜0，故A错误，D错误；
对于B，由图象得，-＜-1，
∴＞1，b＞2a，又a＞0，
∴2=ab＞2a2，
∴a2＜1，与图中的a＞1不符，排除B；
对于C，-＜-1，同理可得a2＜1，
∴0＜a＜1，符合题意．
故选C．
点评：本题考查指数函数与二次函数的图象与性质，考查综合分析与运算能力，属于中档题．
分析：利用指数函数的图象与性质及二次函数的图象与性质即可求得答案．
解答：对于A，∵a＞0，a≠b，ab=2，
∴b=
＞0，∴y=ax2+bx的对称轴x=-
＜0，故A错误，D错误；对于B，由图象得，-
＜-1，∴
＞1，b＞2a，又a＞0，∴2=ab＞2a2，
∴a2＜1，与图中的a＞1不符，排除B；
对于C，-
＜-1，同理可得a2＜1，∴0＜a＜1，符合题意．
故选C．
点评：本题考查指数函数与二次函数的图象与性质，考查综合分析与运算能力，属于中档题．
练习册系列答案
相关题目
若函数y=ax与y=-
在（0，+∞）上都是减函数，则y=ax2+bx在（0，+∞）上是（ ）
| b |
| x |
| A、增函数 | B、减函数 |
| C、先增后减 | D、先减后增 |
