题目内容
有一个翻硬币游戏,开始时硬币正面朝上,然后掷骰子根据下列①、②、③的规则翻动硬币:①骰子出现1点时,不翻动硬币;②出现2,3,4,5点时,翻动一下硬币,使另一面朝上;③出现6点时,如果硬币正面朝上,则不翻动硬币;否则,翻动硬币,使正面朝上.按以上规则,在骰子掷了n次后,硬币仍然正面朝上的概率记为Pn.(Ⅰ)求证:?n∈N*,点(Pn,Pn+1)恒在过定点(
 ,
, ),斜率为
),斜率为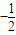 的直线上;
的直线上;(Ⅱ)求数列{Pn}的通项公式Pn;
(Ⅲ)用记号Sn→m表示数列{
 }从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…的前n项和Tn.
}从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…的前n项和Tn.
【答案】分析:(I)把骰子掷了n+1次,硬币仍然正面朝上的概率为Pn+1,此时有两种情况:第n次硬币正面朝上,其概率为Pn,且第n+1次骰子出现1点或6点,硬币不动;第n次硬币反面朝上,其概率为1-Pn,且第n+1次骰子出现2,3,4,5点或6点,求出相应的概率,即可得出结论;
(II)确定{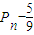 }是首项为
}是首项为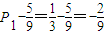 ,公比为
,公比为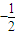 的等比数列,即可求数列的通项;
的等比数列,即可求数列的通项;
(III)解法一:确定S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…,也成等比数列,从而可求和;
解法二:Tn=S1→k+Sk+1→2k+…+S(n-1)k+1→nk=a1+a2+…+ank,可得结论.
解答:(Ⅰ)证明:设把骰子掷了n+1次,硬币仍然正面朝上的概率为Pn+1,此时有两种情况:
①第n次硬币正面朝上,其概率为Pn,且第n+1次骰子出现1点或6点,硬币不动,其概率为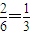 ,
,
因此,此种情况下产生硬币正面朝上的概率为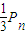 .…(3分)
.…(3分)
②第n次硬币反面朝上,其概率为1-Pn,且第n+1次骰子出现2,3,4,5点或6点,其概率为 ,
,
因此,此种情况下产生硬币正面朝上的概率为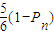 .
.
∴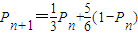 ,变形得
,变形得 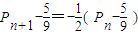 .
.
∴点(Pn,Pn+1)恒在过定点( ,
, ),斜率为
),斜率为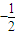 的直线上.…(6分)
的直线上.…(6分)
(Ⅱ)解:P=1,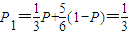 ,
,
又由(Ⅰ)知: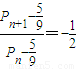 ,
,
∴{ }是首项为
}是首项为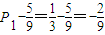 ,公比为
,公比为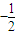 的等比数列,…(8分)
的等比数列,…(8分)
∴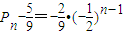 ,
,
故所求通项公式为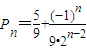 .…(10分)
.…(10分)
(Ⅲ)解法一:由(Ⅱ)知{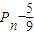 }是首项为
}是首项为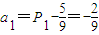 ,公比为
,公比为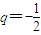 的等比数列,又
的等比数列,又
∵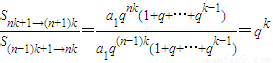 (k∈N*)是常数,
(k∈N*)是常数,
∴S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…,也成等比数列,…(12分)
且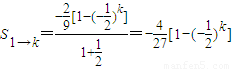
从而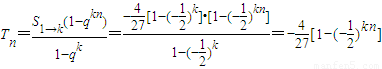 .…(14分)
.…(14分)
解法二:Tn=S1→k+Sk+1→2k+…+S(n-1)k+1→nk=a1+a2+…+ank=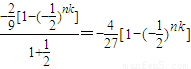 .…(14分)
.…(14分)
点评:本题考查数列与解析几何的综合,考查数列的通项与求和,考查学生分析解决问题的能力,属于中档题.
(II)确定{
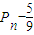 }是首项为
}是首项为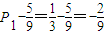 ,公比为
,公比为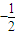 的等比数列,即可求数列的通项;
的等比数列,即可求数列的通项;(III)解法一:确定S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…,也成等比数列,从而可求和;
解法二:Tn=S1→k+Sk+1→2k+…+S(n-1)k+1→nk=a1+a2+…+ank,可得结论.
解答:(Ⅰ)证明:设把骰子掷了n+1次,硬币仍然正面朝上的概率为Pn+1,此时有两种情况:
①第n次硬币正面朝上,其概率为Pn,且第n+1次骰子出现1点或6点,硬币不动,其概率为
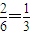 ,
,因此,此种情况下产生硬币正面朝上的概率为
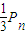 .…(3分)
.…(3分)②第n次硬币反面朝上,其概率为1-Pn,且第n+1次骰子出现2,3,4,5点或6点,其概率为
 ,
,因此,此种情况下产生硬币正面朝上的概率为
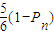 .
.∴
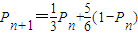 ,变形得
,变形得 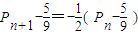 .
.∴点(Pn,Pn+1)恒在过定点(
 ,
, ),斜率为
),斜率为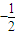 的直线上.…(6分)
的直线上.…(6分)(Ⅱ)解:P=1,
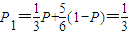 ,
,又由(Ⅰ)知:
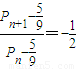 ,
,∴{
 }是首项为
}是首项为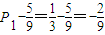 ,公比为
,公比为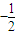 的等比数列,…(8分)
的等比数列,…(8分)∴
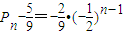 ,
,故所求通项公式为
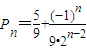 .…(10分)
.…(10分)(Ⅲ)解法一:由(Ⅱ)知{
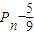 }是首项为
}是首项为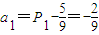 ,公比为
,公比为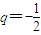 的等比数列,又
的等比数列,又∵
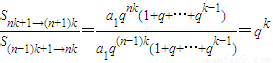 (k∈N*)是常数,
(k∈N*)是常数,∴S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…,也成等比数列,…(12分)
且
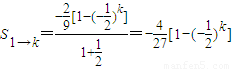
从而
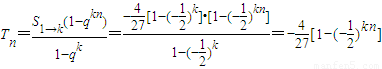 .…(14分)
.…(14分)解法二:Tn=S1→k+Sk+1→2k+…+S(n-1)k+1→nk=a1+a2+…+ank=
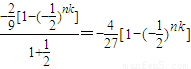 .…(14分)
.…(14分)点评:本题考查数列与解析几何的综合,考查数列的通项与求和,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
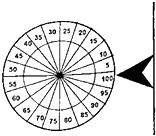 中央二台经济生活频道,在主持人马斌主持的“购物街”栏目中,有一个幸运转盘游戏该游戏规则是这样的:一个木质均匀的标有20等分数字格的转盘(如图),甲、乙两名入选观众每人都有两次转动盘的机会,转盘停止时指针所指的两次数字之和为该人的得分,但超过100分按0分记;且规定:若某人在第一次转动后,认为分值理想,则可以放弃第二次机会,得分按第一次所指的数记,两人中得分多者为优胜,游戏进行中,第一名选手甲通过一次转动后,指针所指的数字是85,试回答以下问题:
中央二台经济生活频道,在主持人马斌主持的“购物街”栏目中,有一个幸运转盘游戏该游戏规则是这样的:一个木质均匀的标有20等分数字格的转盘(如图),甲、乙两名入选观众每人都有两次转动盘的机会,转盘停止时指针所指的两次数字之和为该人的得分,但超过100分按0分记;且规定:若某人在第一次转动后,认为分值理想,则可以放弃第二次机会,得分按第一次所指的数记,两人中得分多者为优胜,游戏进行中,第一名选手甲通过一次转动后,指针所指的数字是85,试回答以下问题: n∈N*,点(Pn,Pn+1)恒在过定点
n∈N*,点(Pn,Pn+1)恒在过定点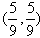 斜率为-
斜率为-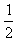 的直线上;
的直线上;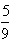 }从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…S(n-1)k+1→nk的前n项和Tn。
}从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…S(n-1)k+1→nk的前n项和Tn。