题目内容
有一个翻硬币游戏,开始时硬币正面朝上,然后掷骰子根据下列①、②、③的规则翻动硬币:①骰子出现1点时,不翻动硬币;②出现2,3,4,5点时,翻动一下硬币,使另一面朝上;③出现6点时,如果硬币正面朝上,则不翻动硬币;否则,翻动硬币,使正面朝上.按以上规则,在骰子掷了n次后,硬币仍然正面朝上的概率记为Pn.
(Ⅰ)求证:?n∈N*,点(Pn,Pn+1)恒在过定点(
,
),斜率为-
的直线上;
(Ⅱ)求数列{Pn}的通项公式Pn;
(Ⅲ)用记号Sn→m表示数列{Pn-
}从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…的前n项和Tn.
(Ⅰ)求证:?n∈N*,点(Pn,Pn+1)恒在过定点(
| 5 |
| 9 |
| 5 |
| 9 |
| 1 |
| 2 |
(Ⅱ)求数列{Pn}的通项公式Pn;
(Ⅲ)用记号Sn→m表示数列{Pn-
| 5 |
| 9 |
(Ⅰ)证明:设把骰子掷了n+1次,硬币仍然正面朝上的概率为Pn+1,此时有两种情况:
①第n次硬币正面朝上,其概率为Pn,且第n+1次骰子出现1点或6点,硬币不动,其概率为
=
,
因此,此种情况下产生硬币正面朝上的概率为
Pn.…(3分)
②第n次硬币反面朝上,其概率为1-Pn,且第n+1次骰子出现2,3,4,5点或6点,其概率为
,
因此,此种情况下产生硬币正面朝上的概率为
(1-Pn).
∴Pn+1=
Pn+
(1-Pn),变形得 Pn+1-
=-
( Pn-
).
∴点(Pn,Pn+1)恒在过定点(
,
),斜率为-
的直线上.…(6分)
(Ⅱ)P0=1,P1=
P0+
(1-P0)=
,
又由(Ⅰ)知:
=-
,
∴{Pn-
}是首项为P1-
=
-
=-
,公比为-
的等比数列,…(8分)
∴Pn-
=-
•(-
)n-1,
故所求通项公式为Pn=
+
.…(10分)
(Ⅲ)解法一:由(Ⅱ)知{Pn-
}是首项为a1=P1-
=-
,公比为q=-
的等比数列,又
∵
=
=qk(k∈N*)是常数,
∴S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…,也成等比数列,…(12分)
且S1→k=
=-
[1-(-
)k]
从而 Tn=
=
=-
[1-(-
)kn].…(14分)
解法二:Tn=S1→k+Sk+1→2k+…+S(n-1)k+1→nk=a1+a2+…+ank=
=-
[1-(-
)nk].…(14分)
①第n次硬币正面朝上,其概率为Pn,且第n+1次骰子出现1点或6点,硬币不动,其概率为
| 2 |
| 6 |
| 1 |
| 3 |
因此,此种情况下产生硬币正面朝上的概率为
| 1 |
| 3 |
②第n次硬币反面朝上,其概率为1-Pn,且第n+1次骰子出现2,3,4,5点或6点,其概率为
| 5 |
| 6 |
因此,此种情况下产生硬币正面朝上的概率为
| 5 |
| 6 |
∴Pn+1=
| 1 |
| 3 |
| 5 |
| 6 |
| 5 |
| 9 |
| 1 |
| 2 |
| 5 |
| 9 |
∴点(Pn,Pn+1)恒在过定点(
| 5 |
| 9 |
| 5 |
| 9 |
| 1 |
| 2 |
(Ⅱ)P0=1,P1=
| 1 |
| 3 |
| 5 |
| 6 |
| 1 |
| 3 |
又由(Ⅰ)知:
Pn+1-
| ||
Pn-
|
| 1 |
| 2 |
∴{Pn-
| 5 |
| 9 |
| 5 |
| 9 |
| 1 |
| 3 |
| 5 |
| 9 |
| 2 |
| 9 |
| 1 |
| 2 |
∴Pn-
| 5 |
| 9 |
| 2 |
| 9 |
| 1 |
| 2 |
故所求通项公式为Pn=
| 5 |
| 9 |
| (-1)n |
| 9•2n-2 |
(Ⅲ)解法一:由(Ⅱ)知{Pn-
| 5 |
| 9 |
| 5 |
| 9 |
| 2 |
| 9 |
| 1 |
| 2 |
∵
| Snk+1→(n+1)k |
| S(n-1)k+1→nk |
| a1qnk(1+q+…+qk-1) |
| a1q(n-1)k(1+q+…+qk-1) |
∴S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…,也成等比数列,…(12分)
且S1→k=
-
| ||||
1+
|
| 4 |
| 27 |
| 1 |
| 2 |
从而 Tn=
| S1→k(1-qkn) |
| 1-qk |
-
| ||||||
1-(-
|
| 4 |
| 27 |
| 1 |
| 2 |
解法二:Tn=S1→k+Sk+1→2k+…+S(n-1)k+1→nk=a1+a2+…+ank=
-
| ||||
1+
|
| 4 |
| 27 |
| 1 |
| 2 |

练习册系列答案
相关题目
 ,
, ),斜率为
),斜率为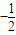 的直线上;
的直线上; }从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…的前n项和Tn.
}从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…的前n项和Tn.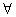 n∈N*,点(Pn,Pn+1)恒在过定点
n∈N*,点(Pn,Pn+1)恒在过定点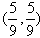 斜率为-
斜率为-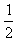 的直线上;
的直线上;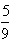 }从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…S(n-1)k+1→nk的前n项和Tn。
}从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…S(n-1)k+1→nk的前n项和Tn。