Question

已知函数f(x)=x

2

3

，x∈[-1，8]，函数g（x）=ax+2，x∈[-1，8]．若存在x∈[-1，8]，使f（x）=g（x）成立．则实数a的取值范围是

 

．

Answer 1

分析：解：分别作出函数f(x)=x

2

3

，x∈[-1，8]，函数g（x）=ax+2，x∈[-1，8]的图象，分析可得，当直线经过点（-1，1）时，a=1；当直线经过点（8，4）时，a=

1

4

，由图得实数a的取值范围．

解答：解：分别作出函数f(x)=x

2

3

，x∈[-1，8]，函数g（x）=ax+2，x∈[-1，8]的图象，

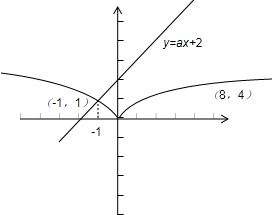
当直线经过点（-1，1）时，a=1；当直线经过点（8，4）时，a=

1

4

．
由图得实数a的取值范围[1，+∞）∪（-∞，

1

4

]．
故填[1，+∞）∪（-∞，

1

4

]．

点评：数形结合是数学解题中常用的思想方法，能够变抽象思维为形象思维，有助于把握数学问题的本质；另外，由于使用了数形结合的方法，很多问题便迎刃而解，且解法简捷．因此，我们既能利用函数图象发现函数性质，又能利用函数图象解决问题．