题目内容
(本题满分10分)已知A、B是椭圆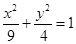 与坐标轴正半轴的两交点,在第一象限的椭圆弧上求一点P,使四边形OPAB的面积最大.
与坐标轴正半轴的两交点,在第一象限的椭圆弧上求一点P,使四边形OPAB的面积最大.
【答案】
当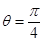 时,d取最大值,从而
时,d取最大值,从而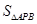 取最大值,这时点P的坐标为
取最大值,这时点P的坐标为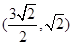 .
.
【解析】本题主要考查了椭圆的简单性质,解答的关键在于利用椭圆的参数方程设出椭圆上一点的坐标,利用三角函数的有界性求最值.设点P的坐标为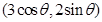 ,其中
,其中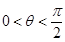 ,∵
,∵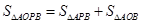 ,其中
,其中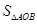 为定值,故只须
为定值,故只须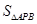 最大即可;
最大即可;
解:设点P的坐标为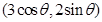 ,其中
,其中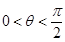 ,
,
∵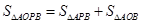 ,其中
,其中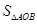 为定值,故只须
为定值,故只须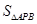 最大即可;
最大即可;
又AB为定长,故只须点P到AB的距离最大即可.AB的方程为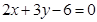 ,点P到AB的距离为
,点P到AB的距离为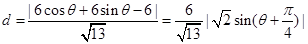
∴当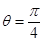 时,d取最大值,从而
时,d取最大值,从而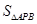 取最大值,这时点P的坐标为
取最大值,这时点P的坐标为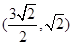 .
.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 .
.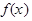 的单调区间;
的单调区间; 且
且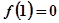 .
. 是偶函数,求函数
是偶函数,求函数 上的最大值和最小值;
上的最大值和最小值; 的取值范围.
的取值范围. ∩
∩ =m,a∥
=m,a∥