Question

已知全集U={小于10的正整数}，A⊆U，B⊆U，且（?_UA）∩B={1，8}A∩B={2，3}，（?_UA）∩（?_UB）={4，6，9}．
（1）求集合A和B．
（2）求（?_RU）∪[?_Z（A∩B）]．（其中R为实数集，Z为整数集）

Answer 1

分析：（1）利用韦恩图，将各个集合进行表示，据图可以写出A，B
（2）直接计算较麻烦，可以显得出[?_Z（A∩B）]?（?_RU），所以（?_RU）∪[?_Z（A∩B）]=?_Z（A∩B）

解答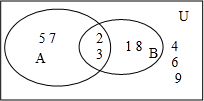：解：（1）利用韦恩图，将各个集合表示如下：
据图可以写出A={}2，3，5，7}，B={1，2，3，8}
（2）A∩B={2，3}，）?_Z（A∩B）={x∈Z|x≠2，且x≠3}．
[?_Z（A∩B）]?（?_RU），所以（?_RU）∪[?_Z（A∩B）]=?_Z（A∩B）={x∈Z|x≠2，且x≠3}．

点评：本题考查集合的基本运算．考查逻辑思维，运算求解能力．容易出错．属于基础题．