题目内容
（2009•大连二模）已知平面内的向量
，
满足：|
|=|
|=
与
1的夹角为
，又
=m
+n
，0≤m≤1，1≤n≤2，则点P的集合所表示的图形面积为（ ）
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| π |
| 3 |
| OP |
| OA |
| OB |
分析：本题考查的知识点是平面区域的面积，处理的方法是根据条件建立平面直角坐标系，将满足不等式表示的可行域表示出来，从而将P点对应的图形描述出来，即可求解．
解答：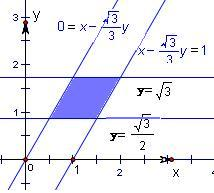
解：不妨以O为原点，以OA方向为x轴正方向，建立坐标系，
则
=（1，0），
=（
，
）
又
=m
+n
，0≤m≤1，1≤n≤2，
令
=（x，y）
则
=（x，y）=（m+
n，
n）
∴
，∴
，
由于0≤m≤1，1≤n≤2，
∴
其表示的平面区域如下图示：
由图可知阴影部分的面积为
×1=
．
故选B．
解：不妨以O为原点，以OA方向为x轴正方向，建立坐标系，则
| OA |
| OB |
| 1 |
| 2 |
| ||
| 2 |
又
| OP |
| OA |
| OB |
令
| OP |
则
| OP |
| 1 |
| 2 |
| ||
| 2 |
∴
|
|
由于0≤m≤1，1≤n≤2，
∴
|
其表示的平面区域如下图示：
由图可知阴影部分的面积为
| ||
| 2 |
| ||
| 2 |
故选B．
点评：平面区域的面积问题是线性规划问题中一类重要题型，在解题时，关键是正确地画出平面区域，然后结合有关面积公式求解．
练习册系列答案
相关题目
（2009•大连二模）如图所示，若向圆x2+y2=2内随机投一点（该点落在圆x2+y2=2内任何一点是等可能的），则所投的点落在圆与y轴及曲线y=x2（x≥0）围成的阴影图形S内部的概率是（ ）