题目内容
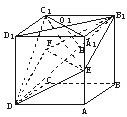 已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1-B1EDF的体积.
已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1-B1EDF的体积.
解:连接A1C1、B1D1交于O1,过O1作O1H⊥B1D于H,
∵EF∥A1C1,
∴A1C1∥平面B1EDF.
∴C1到平面B1EDF的距离就是A1C1到平面B1EDF的距离.
∵平面B1D1D⊥平面B1EDF,
∴O1H⊥平面B1EDF,即O1H为棱锥的高.
∵△B1O1H∽△B1DD1,
∴O1H= =
= a,
a,
VC1-B1EDF
= S
S •O1H
•O1H
= •
• •EF•B1D•O1H
•EF•B1D•O1H
= •
• •
• a•
a• a•
a• a
a
= a3.
a3.
分析:连接A1C1、B1D1交于O1,过O1作O1H⊥B1D于H,说明C1到平面B1EDF的距离就是A1C1到平面B1EDF的距离.求出底面B1EDF的面积,求出高O1H,即可求几何体的体积.
点评:本题考查棱柱、棱锥、棱台的体积,考查空间想象能力,计算能力;是中档题.求体积常见方法有:①直接法(公式法);②分割法;③补形法.
∵EF∥A1C1,
∴A1C1∥平面B1EDF.
∴C1到平面B1EDF的距离就是A1C1到平面B1EDF的距离.
∵平面B1D1D⊥平面B1EDF,
∴O1H⊥平面B1EDF,即O1H为棱锥的高.
∵△B1O1H∽△B1DD1,
∴O1H=
 =
= a,
a,VC1-B1EDF
=
 S
S •O1H
•O1H=
 •
• •EF•B1D•O1H
•EF•B1D•O1H=
 •
• •
• a•
a• a•
a• a
a=
 a3.
a3.分析:连接A1C1、B1D1交于O1,过O1作O1H⊥B1D于H,说明C1到平面B1EDF的距离就是A1C1到平面B1EDF的距离.求出底面B1EDF的面积,求出高O1H,即可求几何体的体积.
点评:本题考查棱柱、棱锥、棱台的体积,考查空间想象能力,计算能力;是中档题.求体积常见方法有:①直接法(公式法);②分割法;③补形法.

练习册系列答案
相关题目
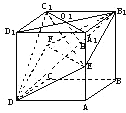 已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1-B1EDF的体积.
已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1-B1EDF的体积.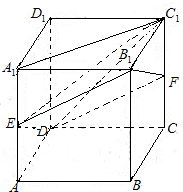 如图,已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱AA1、CC1的中点
如图,已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱AA1、CC1的中点
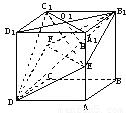 已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1-B1EDF的体积.
已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1-B1EDF的体积.