题目内容
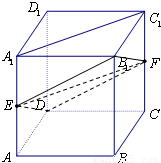
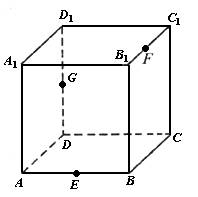
如图,已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱AA1、CC1的中点(1)求证:A1C1∥平面B1EDF;
(2)求四棱锥C1-B1EDF的体积.

【答案】分析:(1)证明A1C1∥平面B1EDF,连接EF,E、F分别AA1、CC1的中点O1,从而可得EF∥A1C1;
(2)取A1C1中点,过O1作O1H⊥B1D于H,根据A1C1∥平面B1EDF,利用等体积转换,即可求得结论.
解答:(1)证明:连接EF,E、F分别AA1、CC1的中点
 O1
O1
∴EF∥A1C1
又EF⊆平面B1EDF,A1C1?平面B1EDF
∴A1C1∥平面B1EDF…(6分)
(2)解:取A1C1中点,过O1作O1H⊥B1D于H
∵A1C1∥平面B1EDF
∴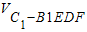 =
= =
=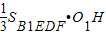 =
=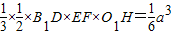 …(12分)
…(12分)
点评:本题考查线面平行,考查四棱锥的体积,解题的关键是掌握线面平行的判定方法,属于中档题.
(2)取A1C1中点,过O1作O1H⊥B1D于H,根据A1C1∥平面B1EDF,利用等体积转换,即可求得结论.
解答:(1)证明:连接EF,E、F分别AA1、CC1的中点
 O1
O1∴EF∥A1C1
又EF⊆平面B1EDF,A1C1?平面B1EDF
∴A1C1∥平面B1EDF…(6分)
(2)解:取A1C1中点,过O1作O1H⊥B1D于H
∵A1C1∥平面B1EDF
∴
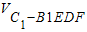 =
= =
=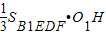 =
=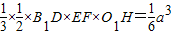 …(12分)
…(12分)点评:本题考查线面平行,考查四棱锥的体积,解题的关键是掌握线面平行的判定方法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




 .
.