题目内容
已知椭圆 的焦距与短轴长相等,点A,B,C都在椭圆C上,且AB、AC分别过两个焦点F1、F2.
的焦距与短轴长相等,点A,B,C都在椭圆C上,且AB、AC分别过两个焦点F1、F2.(I)求椭圆C的离心率;
(II)若直线AB的斜率为2,且线段AB的垂直平分线经过
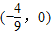 ,求椭圆方程.
,求椭圆方程.
【答案】分析:(I)根据椭圆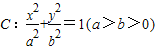 的焦距与短轴长相等,可得b=c,从而可求椭圆C的离心率;
的焦距与短轴长相等,可得b=c,从而可求椭圆C的离心率;
(II)设弦AB中点坐标(m,n),利用直线AB的斜率为2,且线段AB的垂直平分线经过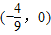 ,求出弦AB中点坐标,从而可求椭圆方程.
,求出弦AB中点坐标,从而可求椭圆方程.
解答:解:(I)∵椭圆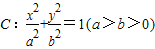 的焦距与短轴长相等,
的焦距与短轴长相等,
∴2c=2b,∴b=c
∴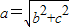 =
=
∴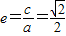 ;
;
(II)设弦AB中点坐标(m,n),则 ,
,
∴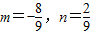 ,
,
又 ,∴c=1,b=1,a2=2
,∴c=1,b=1,a2=2
∴椭圆方程为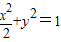 .
.
点评:本题考查椭圆的标准方程与几何性质,考查学生的计算能力,属于中档题.
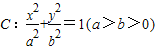 的焦距与短轴长相等,可得b=c,从而可求椭圆C的离心率;
的焦距与短轴长相等,可得b=c,从而可求椭圆C的离心率;(II)设弦AB中点坐标(m,n),利用直线AB的斜率为2,且线段AB的垂直平分线经过
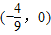 ,求出弦AB中点坐标,从而可求椭圆方程.
,求出弦AB中点坐标,从而可求椭圆方程.解答:解:(I)∵椭圆
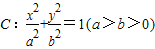 的焦距与短轴长相等,
的焦距与短轴长相等,∴2c=2b,∴b=c
∴
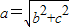 =
=
∴
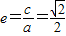 ;
;(II)设弦AB中点坐标(m,n),则
 ,
,∴
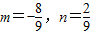 ,
,又
 ,∴c=1,b=1,a2=2
,∴c=1,b=1,a2=2∴椭圆方程为
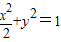 .
.点评:本题考查椭圆的标准方程与几何性质,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 的焦距与短轴长相等,点A,B,C都在椭圆C上,且AB、AC分别过两个焦点F1、F2.
的焦距与短轴长相等,点A,B,C都在椭圆C上,且AB、AC分别过两个焦点F1、F2.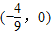 ,求椭圆方程.
,求椭圆方程. 的焦距与短轴长相等,点A,B,C都在椭圆C上,且AB、AC分别过两个焦点F1、F2.
的焦距与短轴长相等,点A,B,C都在椭圆C上,且AB、AC分别过两个焦点F1、F2. ,求椭圆方程.
,求椭圆方程.