题目内容
设正项等比数列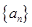 ,
,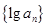 成等差数列,公差
成等差数列,公差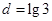 ,且
,且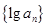 的前三项和为
的前三项和为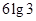 ,则
,则 的通项为
的通项为
A.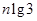 | B.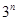 | C.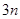 | D.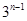 |
B
解析考点:等差数列的性质;等比数列的性质.
分析:由题设条件{lgan} 成等差数列,公差d=lg3,且{lgan} 的前三项和为6lg3,建立方程求出等差数列首项与公差,即可求出lgan,再求an
解:由题意{lgan} 成等差数列,公差d=lg3,且{lgan} 的前三项和为6lg3,
可得3lga1+3lg3=6lg3,
故有lga1=lg3,
所以lgan=lg3+(n-1)lg3=nlg3
即得an=3n
故选B

练习册系列答案
相关题目
 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列 、公差为
、公差为
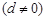 的无穷等差数列.
的无穷等差数列. ,
, 成等比数列,求其公比
成等比数列,求其公比 .
. ,从数列
,从数列 ,从数列
,从数列
 项(设
项(设 )作为一个等比数列的第1项、第2项.求证:当
)作为一个等比数列的第1项、第2项.求证:当 为大于1的正整数时,该数列为
为大于1的正整数时,该数列为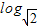 an}的前n项和为Tn.求使Tn>bn的最小正整数n的值.
an}的前n项和为Tn.求使Tn>bn的最小正整数n的值. an}的前n项和为Tn.求使Tn>bn的最小正整数n的值.
an}的前n项和为Tn.求使Tn>bn的最小正整数n的值.