题目内容
如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上.若矩形ORTM的边长OR=7,OM=8,则小正方形的边长为 .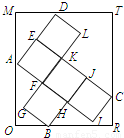
【答案】分析:设∠MAD=θ,小正方形的边长为a,由直角三角形三角函数的定义建立关于a、θ的方程组,并结合同角三角函数的平方关系联解,可得该小正方形的边长.
解答: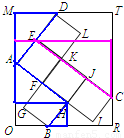 解:设∠MAD=θ,小正方形的边长为a,由直角三角形三角函数的定义,得
解:设∠MAD=θ,小正方形的边长为a,由直角三角形三角函数的定义,得
OR=asinθ+3acosθ=7,OM=2acosθ+2asinθ+acosθ=8
联解,得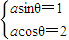 ,即
,即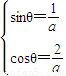
∵sin2θ+cos2θ=1
∴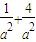 =1,可得a2=5,a=
=1,可得a2=5,a=
故答案为: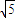
点评:本题给出由五个小正方形接连成的图形内接于长为8、宽为7的矩形中,求小正方形的边长,着重考查了利用三角函数解决平面几何的应用的知识,属于中档题.
解答:
 解:设∠MAD=θ,小正方形的边长为a,由直角三角形三角函数的定义,得
解:设∠MAD=θ,小正方形的边长为a,由直角三角形三角函数的定义,得OR=asinθ+3acosθ=7,OM=2acosθ+2asinθ+acosθ=8
联解,得
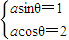 ,即
,即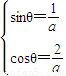
∵sin2θ+cos2θ=1
∴
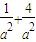 =1,可得a2=5,a=
=1,可得a2=5,a=
故答案为:
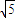
点评:本题给出由五个小正方形接连成的图形内接于长为8、宽为7的矩形中,求小正方形的边长,着重考查了利用三角函数解决平面几何的应用的知识,属于中档题.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
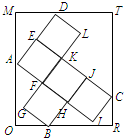 如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上.若矩形ORTM的边长OR=7,OM=8,则小正方形的边长为
如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上.若矩形ORTM的边长OR=7,OM=8,则小正方形的边长为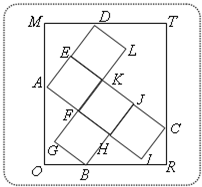 如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上.
如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上.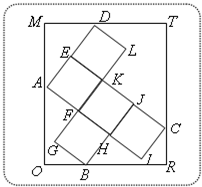 如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上.
如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上.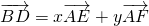 ,求x+y的值;
,求x+y的值; ,求x+y的值;
,求x+y的值;