题目内容
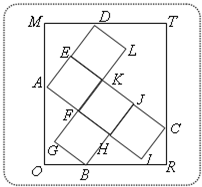 如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上.
如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上.(1)若
| BD |
| AE |
| AF |
(2)若矩形ORTM的边长OR=7,OM=8,试求小正方形的边长;
(3)现向矩形ORTM内任意投出一个点P,求点P落入五个小正方形内的概率.
分析:(1)根据题意,根据向量加法的三角形法则,表示出向量
=
-
=2
-(2
-
)=3
-2
,得到x,y的值,求和即可.
(2)解法一:射线AI、AD的方向分别为x轴、y轴的正向建立平面直角坐标系,设边长为a,写出A,B,C,D以及直线MDT,ODR的方程,运用平行线间的距离公式求解.
解法二:设锐角∠MAD=θ,设小正方形的边长为a,得到
,消去参数θ,求得边长a的值即可.
(3)根据几何概型,点P落入五个小正方形内的概率P(ξ)=
.
| BD |
| AD |
| AB |
| AE |
| AF |
| AE |
| AE |
| AF |
(2)解法一:射线AI、AD的方向分别为x轴、y轴的正向建立平面直角坐标系,设边长为a,写出A,B,C,D以及直线MDT,ODR的方程,运用平行线间的距离公式求解.
解法二:设锐角∠MAD=θ,设小正方形的边长为a,得到
|
(3)根据几何概型,点P落入五个小正方形内的概率P(ξ)=
| 5S正方形 |
| S矩形ORTM |
解答: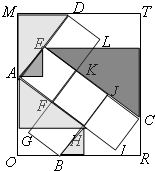 解:(1)由平面向量的加减运算可知
解:(1)由平面向量的加减运算可知
=
-
,而
=2
,
=
+
=2
-
,故
=
-
=2
-(2
-
)=3
-2
.注意到
、
不共线,根据平面向量基本定理,比较
=x
+y
与
=3
-2
可知x=3,y=-2,x+y=1.
(2)解法一:因为
⊥
以射线AI、AD的方向分别为x轴、y轴的正向建立平面直角坐标系,设小正方形的边长为a得A(0,0)、B(2a,-a)、C(3a,a)、D(0,2a).设直线MDT的斜率为k,则MDT:y=kx+2a(k>0),OBR:y=kx-a(2k+1),MAO:y=-
x,TCR:y=-
x+a+
.由此可得直线MDT、OBR之间的距离是
=8,直线MAO、TCR之间的距离是
=7,由此可解得k=
,,a=
,即小正方形的边长为
.
解法二:设锐角∠MAD=θ,设小正方形的边长为a,则由右图可得
相减得
消去θ解得边长为a=
.
(3)设“向矩形ORTM内任意投出T(-1,1)一个点P,点P落入五个小正方形内”为事件ξ,
由几何概型可知,点P落入五个小正方形内的概率 P(ξ)=
=
.
 解:(1)由平面向量的加减运算可知
解:(1)由平面向量的加减运算可知| BD |
| AD |
| AB |
| AD |
| AE |
| AB |
| AH |
| HB |
| AF |
| AE |
| BD |
| AD |
| AB |
| AE |
| AF |
| AE |
| AE |
| AF |
| AE |
| AF |
| BD |
| AE |
| AF |
| BD |
| AE |
| AF |
(2)解法一:因为
| AE |
| AF |
| 1 |
| k |
| 1 |
| k |
| 3a |
| k |
| a(2k+3) | ||
|
a(
| ||||
|
| 1 |
| 2 |
| 5 |
| 5 |
解法二:设锐角∠MAD=θ,设小正方形的边长为a,则由右图可得
|
|
| 5 |
(3)设“向矩形ORTM内任意投出T(-1,1)一个点P,点P落入五个小正方形内”为事件ξ,
由几何概型可知,点P落入五个小正方形内的概率 P(ξ)=
| 5S正方形 |
| S矩形ORTM |
| 25 |
| 56 |
点评:此题考查平面向量基本道理和数量积的运算,以及建立坐标系,参数方程解决几何问题,还考查了几何概型,属于较难的题目,应该灵活掌握.

练习册系列答案
相关题目
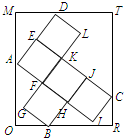 如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上.若矩形ORTM的边长OR=7,OM=8,则小正方形的边长为
如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上.若矩形ORTM的边长OR=7,OM=8,则小正方形的边长为 如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上.
如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上.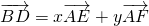 ,求x+y的值;
,求x+y的值;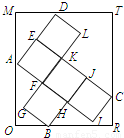
 ,求x+y的值;
,求x+y的值;