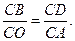题目内容
(本题满分16分)
如图,直角三角形ABC中,∠B=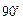 ,AB=1,B
,AB=1,B C=
C=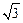 .点M,N分别在边AB和AC
.点M,N分别在边AB和AC
上(M点和B点不重合),将△AMN沿MN翻折,△AMN变为△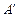 MN,使顶点
MN,使顶点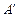 落
落
在边BC上(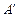 点和B点不重合).设∠AMN=
点和B点不重合).设∠AMN=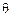 .
.
(1) 用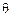 表示线段
表示线段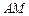 的长度,并写出
的长度,并写出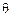 的取值范围;
的取值范围;
(2) 求线段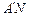 长度的最小值.
长度的最小值.
如图,直角三角形ABC中,∠B=
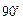 ,AB=1,B
,AB=1,B C=
C=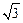 .点M,N分别在边AB和AC
.点M,N分别在边AB和AC 上(M点和B点不重合),将△AMN沿MN翻折,△AMN变为△
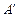 MN,使顶点
MN,使顶点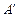 落
落在边BC上(
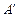 点和B点不重合).设∠AMN=
点和B点不重合).设∠AMN=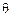 .
.(1) 用
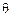 表示线段
表示线段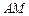 的长度,并写出
的长度,并写出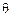 的取值范围;
的取值范围;(2) 求线段
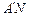 长度的最小值.
长度的最小值. 解:(1)设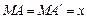 ,则
,则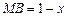 .(2分)
.(2分)
在Rt△MB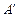 中,
中,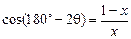 , (4分)
, (4分)
∴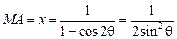 . (5分)
. (5分)
∵点M在线段AB上,M点和B点不重合,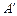 点和B点不重合,
点和B点不重合,
∴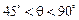 .(7分)
.(7分)
(2)在△AMN中,∠ANM=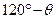 ,(8分)
,(8分)
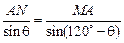 ,(9分)
,(9分)
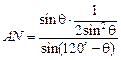 =
=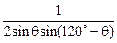 .(10分)
.(10分)
令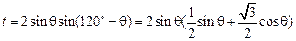 =
=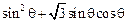
=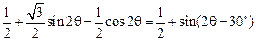 .(13分)
.(13分)
∵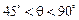 , ∴
, ∴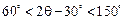 . (14分)
. (14分)
当且仅当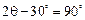 ,
,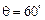 时,
时,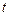 有最大值
有最大值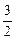 ,(15分)
,(15分)
∴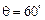 时,
时,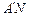 有最小值
有最小值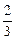 .(16分)
.(16分)
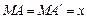 ,则
,则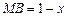 .(2分)
.(2分)在Rt△MB
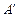 中,
中,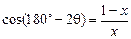 , (4分)
, (4分)∴
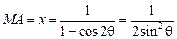 . (5分)
. (5分)∵点M在线段AB上,M点和B点不重合,
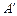 点和B点不重合,
点和B点不重合,∴
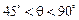 .(7分)
.(7分)(2)在△AMN中,∠ANM=
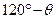 ,(8分)
,(8分)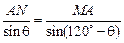 ,(9分)
,(9分)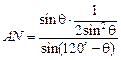 =
=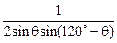 .(10分)
.(10分)令
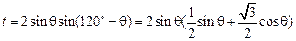 =
=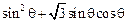
=
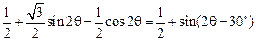 .(13分)
.(13分)∵
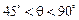 , ∴
, ∴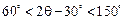 . (14分)
. (14分)当且仅当
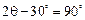 ,
,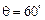 时,
时,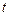 有最大值
有最大值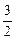 ,(15分)
,(15分)∴
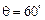 时,
时,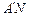 有最小值
有最小值 .(16分)
.(16分)略

练习册系列答案
相关题目
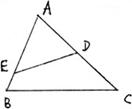
 于两点,与C1交于两点,这四点按纵坐标从大到小依次为A、B、C、D.
于两点,与C1交于两点,这四点按纵坐标从大到小依次为A、B、C、D.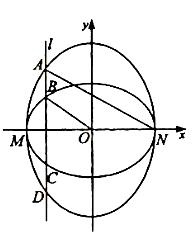
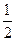 ,求|BC|与|AD|的比值;
,求|BC|与|AD|的比值;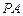 与圆
与圆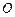 相切于点
相切于点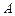 ,半径
,半径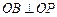 ,
,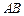 交
交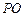 于
于 点
点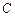 ,
,
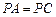 ;
;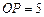 ,求
,求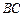 的长度.
的长度.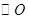 的弦
的弦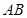 交半径
交半径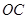 于点
于点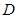 ,若
,若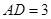 ,
,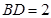 ,且
,且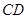 的长为 .
的长为 .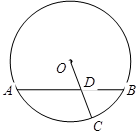
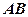
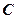 是内接于⊙O,
是内接于⊙O,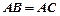 ,
,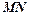 切⊙O于点
切⊙O于点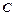 ,弦
,弦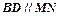 ,
,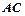
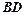 相交于点
相交于点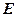 .
.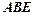 ≌Δ
≌Δ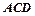 ;
;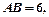
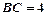 ,求
,求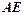 .
.
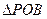 中,
中,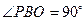 ,以
,以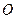 为圆心、
为圆心、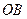 为半径作圆弧交
为半径作圆弧交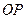 于
于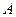 点.若弧AB等分△POB的面积,且∠AOB=
点.若弧AB等分△POB的面积,且∠AOB=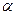 弧度,则( )
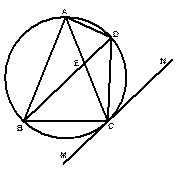
弧度,则( ) 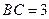 过
过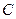 作圆的切线
作圆的切线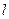 ,过A作
,过A作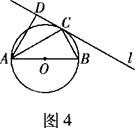
 =∠C,则AE=" "
=∠C,则AE=" "