题目内容
在复平面内,  是原点,向量
是原点,向量 对应的复数是
对应的复数是 ,
, =2+i。
=2+i。
(Ⅰ)如果点A关于实轴的对称点为点B,求向量 对应的复数
对应的复数 和
和 ;
;
(Ⅱ)复数 ,
, 对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
 是原点,向量
是原点,向量 对应的复数是
对应的复数是 ,
, =2+i。
=2+i。(Ⅰ)如果点A关于实轴的对称点为点B,求向量
 对应的复数
对应的复数 和
和 ;
;(Ⅱ)复数
 ,
, 对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。(Ⅰ) =
=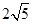 (Ⅱ)见解析
(Ⅱ)见解析
 =
=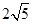 (Ⅱ)见解析
(Ⅱ)见解析第一问中利用复数的概念可知得到由题意得,A(2,1) ∴B(2,-1) ∴  ="(0,-2)" ∴
="(0,-2)" ∴ =-2i ∵
=-2i ∵ 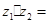 (2+i)(-2i)=2-4i, ∴
(2+i)(-2i)=2-4i, ∴  =
=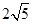
第二问中,由题意得, =(2,1) ∴
=(2,1) ∴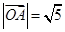
同理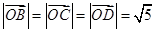 ,所以A、B、C、D四点到原点O的距离相等,
,所以A、B、C、D四点到原点O的距离相等,
∴A、B、C、D四点在以O为圆心,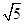 为半径的圆上
为半径的圆上
(Ⅰ)由题意得,A(2,1) ∴B(2,-1) ∴ ="(0,-2)" ∴
="(0,-2)" ∴ =-2i 3分
=-2i 3分
∵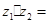 (2+i)(-2i)=2-4i, ∴
(2+i)(-2i)=2-4i, ∴  =
=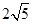 2分
2分
(Ⅱ)A、B、C、D四点在同一个圆上。 2分
证明:由题意得, =(2,1) ∴
=(2,1) ∴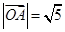
同理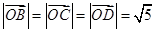 ,所以A、B、C、D四点到原点O的距离相等,
,所以A、B、C、D四点到原点O的距离相等,
∴A、B、C、D四点在以O为圆心,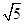 为半径的圆上
为半径的圆上
 ="(0,-2)" ∴
="(0,-2)" ∴ =-2i ∵
=-2i ∵ 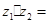 (2+i)(-2i)=2-4i, ∴
(2+i)(-2i)=2-4i, ∴  =
=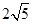
第二问中,由题意得,
 =(2,1) ∴
=(2,1) ∴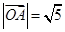
同理
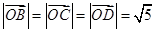 ,所以A、B、C、D四点到原点O的距离相等,
,所以A、B、C、D四点到原点O的距离相等,∴A、B、C、D四点在以O为圆心,
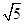 为半径的圆上
为半径的圆上(Ⅰ)由题意得,A(2,1) ∴B(2,-1) ∴
 ="(0,-2)" ∴
="(0,-2)" ∴ =-2i 3分
=-2i 3分∵
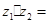 (2+i)(-2i)=2-4i, ∴
(2+i)(-2i)=2-4i, ∴  =
=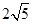 2分
2分(Ⅱ)A、B、C、D四点在同一个圆上。 2分
证明:由题意得,
 =(2,1) ∴
=(2,1) ∴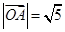
同理
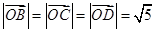 ,所以A、B、C、D四点到原点O的距离相等,
,所以A、B、C、D四点到原点O的距离相等,∴A、B、C、D四点在以O为圆心,
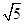 为半径的圆上
为半径的圆上
练习册系列答案
相关题目
 ,复数z=
,复数z= .
. 是实数,复数
是实数,复数 (
( 为虚数单位),则
为虚数单位),则 的最小值为__________.
的最小值为__________. 是关于x的实系数方程
是关于x的实系数方程 的一个复数根,则( )
的一个复数根,则( )


 .
. ,则复数
,则复数 的共轭复数为( )
的共轭复数为( )



 是纯虚数,
是纯虚数, 是实数,那么
是实数,那么



 满足
满足  ,(
,( 为虚数单位),则
为虚数单位),则 的虚部为 ▲ .
的虚部为 ▲ . 表示为
表示为 是虚数单位)的形式,则
是虚数单位)的形式,则 .
. 满足:
满足: ;则
;则 ( )
( )


