题目内容
(Ⅰ)若椭圆上任一点到两个焦点(-2,0),(2,0)的距离之和为6,求椭圆的标准方程;
(Ⅱ)若椭圆过(2,0),离心率为
,求椭圆的标准方程.
(Ⅱ)若椭圆过(2,0),离心率为
| ||
| 2 |
分析:(Ⅰ)由题意可得:c=2,并且得到椭圆的焦点在x轴上,再根据椭圆的定义得到a=3,进而由a,b,c的关系求出b的值得到椭圆的方程.
(Ⅱ)由于椭圆的焦点位置未定,故需要进行分类讨论,进而可求椭圆的标准方程.
(Ⅱ)由于椭圆的焦点位置未定,故需要进行分类讨论,进而可求椭圆的标准方程.
解答:解:(Ⅰ)∵两个焦点的坐标分别是(-2,0),(2,0),
∴椭圆的焦点在横轴上,并且c=2,
∴由椭圆的定义可得:2a=6,即a=3,
∴由a,b,c的关系解得b2=32-22=5,
故椭圆的标准方程为
+
=1;
(Ⅱ)由于离心率e=
=
,得c2=
a2,b2=a2-c2=
a2,
当椭圆焦点在x轴上时,a=2,∴b2=1,∴所求椭圆方程为
+y2=1;
当椭圆焦点在y轴上时,b=2,∴a2=16,∴所求椭圆方程为
+
=1.
∴椭圆的焦点在横轴上,并且c=2,
∴由椭圆的定义可得:2a=6,即a=3,
∴由a,b,c的关系解得b2=32-22=5,
故椭圆的标准方程为
| x2 |
| 9 |
| y2 |
| 5 |
(Ⅱ)由于离心率e=
| c |
| a |
| ||
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
当椭圆焦点在x轴上时,a=2,∴b2=1,∴所求椭圆方程为
| x2 |
| 4 |
当椭圆焦点在y轴上时,b=2,∴a2=16,∴所求椭圆方程为
| x2 |
| 4 |
| y2 |
| 16 |
点评:本题主要考查椭圆的标准方程与椭圆的定义,以及考查椭圆的简单性质,考查分类讨论的数学思想,此题属于基础题.

练习册系列答案
相关题目
 以极点为原点,极轴为
以极点为原点,极轴为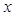 轴非负半轴,建立平面直角坐标 系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标 系,且两坐标系取相同的单位长度.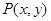 ,求
,求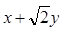 的取值范围;
的取值范围;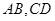 交于点
交于点 ,且直线
,且直线 与
与 的倾斜角互补,
的倾斜角互补, .
.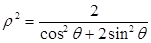
 轴非负半轴,建立平面直角坐标 系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标 系,且两坐标系取相同的单位长度. ,求
,求 的取值范围;
的取值范围;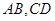 交于点
交于点 ,且直线
,且直线 与
与 的倾斜角互补,
的倾斜角互补, .
.
 轴非负半轴,建立平面直角坐标 系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标 系,且两坐标系取相同的单位长度. ,求
,求 的取值范围;
的取值范围; 交于点
交于点 ,且直线
,且直线 与
与 的倾斜角互补,
的倾斜角互补,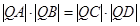 .
.