题目内容
极坐标系中椭圆C的方程为
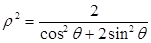
以极点为原点,极轴为 轴非负半轴,建立平面直角坐标 系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标 系,且两坐标系取相同的单位长度.
(Ⅰ)求该椭圆的直角标方程;若椭圆上任一点坐标为 ,求
,求 的取值范围;
的取值范围;
(Ⅱ)若椭圆的两条弦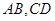 交于点
交于点 ,且直线
,且直线 与
与 的倾斜角互补,
的倾斜角互补,
求证: .
.
【答案】
(Ⅰ) (Ⅱ)详见解析
(Ⅱ)详见解析
【解析】
试题分析:将椭圆的极坐标方程转化为一般标准方程,再利用换元法求范围,利用参数方程代入,计算得到结果.
试题解析:(Ⅰ)该椭圆的直角标方程为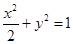 ,
2分
,
2分
设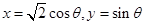 ,
,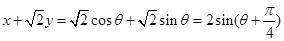
所以 的取值范围是
的取值范围是 4分
4分
(Ⅱ)设直线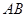 的倾斜角为
的倾斜角为 ,直线
,直线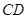 的倾斜角为
的倾斜角为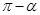 ,
,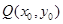
则直线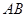 的参数方程为
的参数方程为 (
(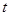 为参数),(5分)
为参数),(5分)
代入 得:
得: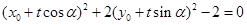
即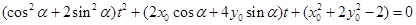 7分
7分
同理 9分
9分
所以 (10分)
(10分)
考点:极坐标、参数方程,换元法应用.

练习册系列答案
相关题目
 以极点为原点,极轴为
以极点为原点,极轴为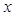 轴非负半轴,建立平面直角坐标 系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标 系,且两坐标系取相同的单位长度.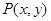 ,求
,求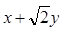 的取值范围;
的取值范围;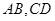 交于点
交于点 ,且直线
,且直线 与
与 的倾斜角互补,
的倾斜角互补, .
.
 轴非负半轴,建立平面直角坐标 系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标 系,且两坐标系取相同的单位长度. ,求
,求 的取值范围;
的取值范围; 交于点
交于点 ,且直线
,且直线 与
与 的倾斜角互补,
的倾斜角互补,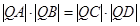 .
.