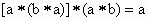题目内容
(2007
·广东)设 ,
, 是
是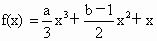 (a,b∈R,a>0)的两个极值点,f(x)的导函数是
(a,b∈R,a>0)的两个极值点,f(x)的导函数是 .
.
(1)
如果 ,求证:
,求证: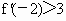 ;
;
(2)
如果 ,
, ,求b的取值范围;
,求b的取值范围;
(3)
如果a≥2,且 ,x∈(
,x∈(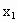 ,
,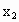 )时,函数
)时,函数 的最小值为h(a),求h(a)的最大值.
的最小值为h(a),求h(a)的最大值.
答案:略
解析:
解析:
|
(1)  是方程 是方程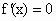 的两个根. 的两个根.
由 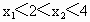 且a>0得 且a>0得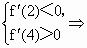
①×(- 3)+②得4a-2b>0.∴ 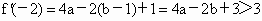
(2) 由第(1)问知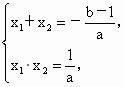
由  ,两式相除得 ,两式相除得
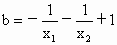 . .
①当 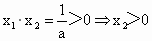 , ,
∴  ,即 ,即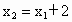 . .
∴ 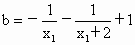 , ,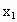 ∈(0,2). ∈(0,2).
令函数 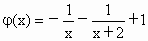 ,∵x>0,则 ,∵x>0,则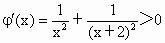 , ,
∴ φ(x)在(0,+∞)上是增函数.∴当 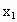 ∈(0,2)时, ∈(0,2)时,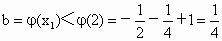 ,即 ,即 . .
②当  ∴ ∴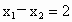 ,即 ,即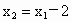 . .
∴ 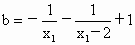 , ,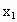 ∈(-2,0). ∈(-2,0).
令函数 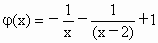 ,若x<0则同理可证φ(x)在(-∞,0)上是增函数. ,若x<0则同理可证φ(x)在(-∞,0)上是增函数.
∴当 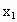 ∈(-2,0)时, ∈(-2,0)时,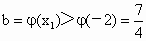 . .
综①②所述, b的取值范围是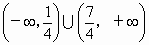 . .
(3 )∵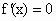 的两个根是 的两个根是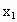 , , , ,
∴可设  . .
∴ 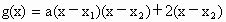
∴ 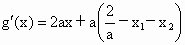 . .
令 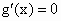 ,∵a≥2,∴ ,∵a≥2,∴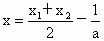 . .
由题意知 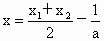 时,g(x)取最小值 时,g(x)取最小值
∴ 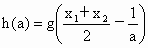
∴  . .
令 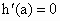 , ,
∴  . .
∴ 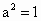 . .
由题意知 a=2时,h(a)取最大值且等于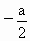 . . |

练习册系列答案
相关题目
 ,
,

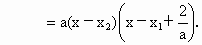
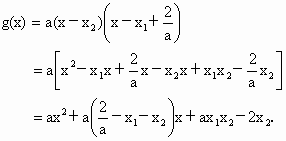

 的半焦距为c,直线l过(0,a)和(b,0),已知原点到直线l的距离等于
的半焦距为c,直线l过(0,a)和(b,0),已知原点到直线l的距离等于 ,则椭圆的离心率为
,则椭圆的离心率为



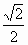
 S,对于有序元素对(a,b),在S中有唯一确定的元素
S,对于有序元素对(a,b),在S中有唯一确定的元素 与之对应).若对任意的a,b
与之对应).若对任意的a,b ,则对任意的a,b
,则对任意的a,b