题目内容
定义在R上的函数y=f(x),对任意不等的实数x1,x2都有[f(x1)-f(x2)](x1-x2)<0成立,又函数y=f(x-1)的图象关于点(1,0)对称,若不等式f(
-2x)+f(2y-
)≤0成立,则当1≤x<4时,
的取值范围是( )
| x | 2 |
| y | 2 |
| y |
| x |
A、(-
| ||
| B、(-∞,1] | ||
C、[-
| ||
D、[-
|
分析:依题意知,y=f(x)为R上的减函数,且为奇函数,于是由f(x2-2x)+f(2y-y2)≤0⇒x2-2x≥y2-2y⇒(x-y)(x+y-2)≥0,利用线性规划的知识即可求得当1≤x<4时,
的取值范围.
| y |
| x |
解答:解:∵函数y=f(x),对任意不等的实数x1,x2都有[f(x1)-f(x2)](x1-x2)<0成立,
∴y=f(x)为R上的减函数;
又函数y=f(x-1)的图象关于点(1,0)对称,
∴函数y=f(x)的图象关于点(0,0)对称,
∴函数y=f(x)为奇函数;
又f(x2-2x)+f(2y-y2)≤0,
∴x2-2x≥y2-2y,
(x-y)(x+y-2)≥0,
∴
或
,
令k=
=
,作出线性区域图如下(两直线x-y=0与x+y-2=0相交的左右区域):
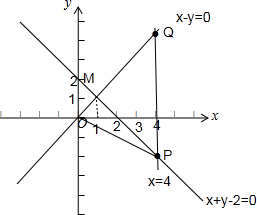
当x=1时,y=1,直线x-y=0上的点M(1,1),此时kmax=kOM=
=1,
当x=4时,y=2-4=-2,直线x+y-2=0上的点P(4,-2),此时k=
=-
,
∵1≤x<4,
∴-
<k≤1,
故选:A.
∴y=f(x)为R上的减函数;
又函数y=f(x-1)的图象关于点(1,0)对称,
∴函数y=f(x)的图象关于点(0,0)对称,
∴函数y=f(x)为奇函数;
又f(x2-2x)+f(2y-y2)≤0,
∴x2-2x≥y2-2y,
(x-y)(x+y-2)≥0,
∴
|
|
令k=
| y |
| x |
| y-0 |
| x-0 |

当x=1时,y=1,直线x-y=0上的点M(1,1),此时kmax=kOM=
| 1-0 |
| 1-0 |
当x=4时,y=2-4=-2,直线x+y-2=0上的点P(4,-2),此时k=
| -2-0 |
| 4-0 |
| 1 |
| 2 |
∵1≤x<4,
∴-
| 1 |
| 2 |
故选:A.
点评:本题考查抽象函数及其应用,着重考查函数的单调性与奇偶性的综合应用,突出考查线性规划,考查等价转化思想与数形结合思想,属于难题.

练习册系列答案
相关题目