题目内容
已知椭圆C中心为坐标原点O,焦点在x轴上,短轴长为2
,离心率为
(1)求椭圆C的方程;
(2)直线l:y=kx+m与椭圆C交于不同两点P,Q,且OP⊥OQ,求点O到直线l的距离.
| 21 |
| 1 |
| 2 |
(1)求椭圆C的方程;
(2)直线l:y=kx+m与椭圆C交于不同两点P,Q,且OP⊥OQ,求点O到直线l的距离.
(1)设椭圆C的方程为
+
=1(a>b>0).
由题意可得
,解得
,
∴椭圆C的方程为
+
=1.
(2)设A(x1,y1),B(x2,y2).
联立
,消去y得到(3+4k2)x2+8kmx+4m2-84=0.
∵△>0,∴64k2m2-16(3+4k2)(m2-21)=0,化为m2=21+28k2.(*)
∴x1+x2=
,x1x2=
.(**)
∵OP⊥OQ,∴
•
=0.
∴x1x2+y1y2=0.
又y1y2=(kx1+m)(kx2+m),
∴(1+k2)x1x2+km(x1+x2)+m2=0.
把(**)代入可得
+
+m2=0.
化为m2=12+12k2=12(1+k2),∴
=2
.
∴点O到直线l的距离d=
=2
.
| x2 |
| a2 |
| y2 |
| b2 |
由题意可得
|
|
∴椭圆C的方程为
| x2 |
| 28 |
| y2 |
| 21 |
(2)设A(x1,y1),B(x2,y2).
联立
|
∵△>0,∴64k2m2-16(3+4k2)(m2-21)=0,化为m2=21+28k2.(*)
∴x1+x2=
| -8km |
| 3+4k2 |
| 4m2-84 |
| 3+4k2 |
∵OP⊥OQ,∴
| OP |
| OQ |
∴x1x2+y1y2=0.
又y1y2=(kx1+m)(kx2+m),
∴(1+k2)x1x2+km(x1+x2)+m2=0.
把(**)代入可得
| (1+k2)(4m2-84) |
| 3+4k2 |
| -8k2m2 |
| 3+4k2 |
化为m2=12+12k2=12(1+k2),∴
| |m| | ||
|
| 3 |
∴点O到直线l的距离d=
| |m| | ||
|
| 3 |

练习册系列答案
相关题目
 ,离心率为
,离心率为 ,
,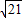 ,离心率为
,离心率为