题目内容
已知椭圆C中心为坐标原点O,焦点在x轴上,短轴长为2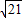 ,离心率为
,离心率为
(1)求椭圆C的方程;
(2)直线l:y=kx+m与椭圆C交于不同两点P,Q,且OP⊥OQ,求点O到直线l的距离.
【答案】分析:(1)设椭圆C的方程为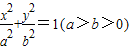 .由题意可得
.由题意可得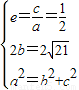 ,解出即可.
,解出即可.
(2)直线l的方程与椭圆方程联立即可得到根与系数的关系,再利用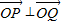 ?
?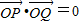 ,及点到直线的距离公式即可得出.
,及点到直线的距离公式即可得出.
解答:解:(1)设椭圆C的方程为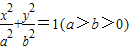 .
.
由题意可得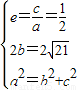 ,解得
,解得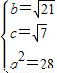 ,
,
∴椭圆C的方程为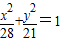 .
.
(2)设A(x1,y1),B(x2,y2).
联立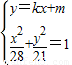 ,消去y得到(3+4k2)x2+8kmx+4m2-84=0.
,消去y得到(3+4k2)x2+8kmx+4m2-84=0.
∵△>0,∴64k2m2-16(3+4k2)(m2-21)=0,化为m2=21+28k2.(*)
∴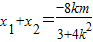 ,
,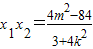 .(**)
.(**)
∵OP⊥OQ,∴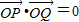 .
.
∴x1x2+y1y2=0.
又y1y2=(kx1+m)(kx2+m),
∴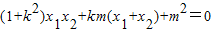 .
.
把(**)代入可得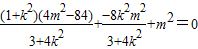 .
.
化为m2=12+12k2=12(1+k2),∴ .
.
∴点O到直线l的距离d=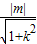 =
=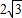 .
.
点评:本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、向量垂直与数量积得关系、点到直线的距离公式等基础知识与基本技能,考查了推理能力和计算能力.
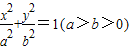 .由题意可得
.由题意可得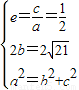 ,解出即可.
,解出即可.(2)直线l的方程与椭圆方程联立即可得到根与系数的关系,再利用
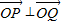 ?
?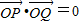 ,及点到直线的距离公式即可得出.
,及点到直线的距离公式即可得出.解答:解:(1)设椭圆C的方程为
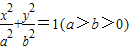 .
.由题意可得
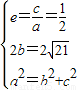 ,解得
,解得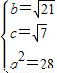 ,
,∴椭圆C的方程为
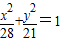 .
.(2)设A(x1,y1),B(x2,y2).
联立
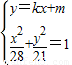 ,消去y得到(3+4k2)x2+8kmx+4m2-84=0.
,消去y得到(3+4k2)x2+8kmx+4m2-84=0.∵△>0,∴64k2m2-16(3+4k2)(m2-21)=0,化为m2=21+28k2.(*)
∴
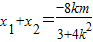 ,
,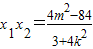 .(**)
.(**)∵OP⊥OQ,∴
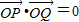 .
.∴x1x2+y1y2=0.
又y1y2=(kx1+m)(kx2+m),
∴
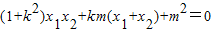 .
.把(**)代入可得
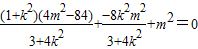 .
.化为m2=12+12k2=12(1+k2),∴
 .
.∴点O到直线l的距离d=
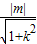 =
=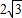 .
.点评:本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、向量垂直与数量积得关系、点到直线的距离公式等基础知识与基本技能,考查了推理能力和计算能力.

练习册系列答案
相关题目
 ,离心率为
,离心率为 ,
,