题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)求证:当![]() 时,
时,![]() .
.
【答案】(1)见解析(2)见解析
【解析】
(1)根据题意,对函数![]() 求导,利用导数研究函数单调性问题,分情况讨论函数单调性;
求导,利用导数研究函数单调性问题,分情况讨论函数单调性;
(2)解法一:转化思想![]() ,等价于
,等价于![]() 设
设![]() ,只须证当
,只须证当![]() 时,
时,![]() 成立,即可证明.
成立,即可证明.
解法二:导出![]() 的不等式,要证
的不等式,要证![]() ,只须证
,只须证![]() ;
;
解法三:同解法二,只须证![]() ,构造函数,运用放缩法,证明不等式;
,构造函数,运用放缩法,证明不等式;
解法四:要证![]() ,只须证
,只须证![]() .因为
.因为![]() ,所以
,所以![]() (
(![]() )所以只须证
)所以只须证![]() ,即证
,即证![]() ;
;
解法五:要证![]() ,只须证
,只须证![]() ,结合解法四的放缩法,因为
,结合解法四的放缩法,因为![]() ,所以
,所以![]() (
(![]() )再结合解法三的放缩法,又
)再结合解法三的放缩法,又![]() ,即可证明.
,即可证明.
解法一:(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]() .
.
当![]() 时,
时,![]() 在
在![]() 恒成立,故
恒成立,故![]() 在
在![]() 单调递增.
单调递增.
当![]() 时,由
时,由![]() 得
得![]() .
.
当 时,
时,![]() ;当
;当 时,
时,![]() .
.
所以![]() 在
在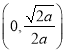 单调递增,在
单调递增,在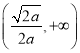 单调递减.
单调递减.
综上,当![]() 时,
时,![]() 在
在![]() 单调递增.
单调递增.
当![]() 时,
时,![]() 在
在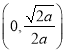 单调递增,在
单调递增,在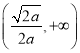 单调递减.
单调递减.
(2)由![]() ,等价于
,等价于![]() .
.
设![]() ,只须证当
,只须证当![]() 时,
时,![]() 成立.
成立.
因为![]() ,
,![]()
由![]() ,得
,得![]() 有异号两根,令其正根为
有异号两根,令其正根为![]() ,
,
则![]() ,从而
,从而![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
所以![]() 的最大值为
的最大值为![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
所以![]() .
.
所以![]() .
.
所以![]() ,所以当
,所以当![]() 时,
时,![]() .
.
解法二:(1)同解法一.
(2)要证![]() ,只须证
,只须证![]() .①
.①
设![]() ,则
,则![]()
令![]() ,则
,则![]() ,
,![]() 在
在![]() 单调递减,
单调递减,
又![]() ,
,![]() ,
,
所以存在惟一的![]() ,使
,使![]() .
.
当![]() 时,
时,![]() ,从而
,从而![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减.
单调递减.
所以![]() 的最大值为
的最大值为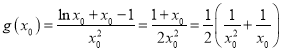 ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,所以①式成立,所以当
,所以①式成立,所以当![]() 时,
时,![]() .
.
解法三:(1)同解法一.
(2)要证![]() ,只须证
,只须证![]() .①
.①
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
所以![]() ,所以
,所以![]() .
.
所以![]() ,
,
要证①式成立,只须证![]() .②
.②
设![]() ,则
,则![]()
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
所以![]() 的最大值为
的最大值为![]() ,
,
又![]() ,所以②式成立,
,所以②式成立,
所以当![]() 时,
时,![]() .
.
解法四:(1)同解法一.
(2)要证![]() ,只须证
,只须证![]() .
.
因为![]() ,所以
,所以![]() (
(![]() )
)
所以只须证![]() ,即证
,即证![]() .①
.①
设![]() ,
,
则![]() (
(![]() ),
),
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
所以![]() ,所以①式成立,
,所以①式成立,
所以当![]() 时,
时,![]() .
.
解法五:(1)同解法一.
(2)要证![]() ,只须证
,只须证![]() .
.
因为![]() ,所以
,所以![]() (
(![]() )
)
又![]() (证明过程见解法三,考生未写出证明过程扣1分)
(证明过程见解法三,考生未写出证明过程扣1分)
所以只须证![]() ,即证
,即证![]() ,这显然成立.
,这显然成立.
所以当![]() 时,
时,![]() .
.