题目内容
已知直线l是抛物线y=x2的一条切线,且l与直线2x-y+4=0平行,则直线l的方程是( )A.2x-y+3=0
B.2x-y-3=0
C.2x-y+1=0
D.2x-y-1=0
【答案】分析:根据切线与直线2x-y+4=0的平行,可利用待定系数法设出切线,然后与抛物线联立方程组,使方程只有一解即可.
解答:解:由题意可设切线方程为2x-y+m=0
得方程组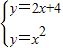 得x2-2x-m=0
得x2-2x-m=0
△=4+4m=0解得m=-1,
∴切线方程为2x-y-1=0,
故选D
点评:本题主要考查了两条直线平行的判定,以及直线的一般式方程,属于基础题.
解答:解:由题意可设切线方程为2x-y+m=0
得方程组
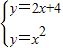 得x2-2x-m=0
得x2-2x-m=0△=4+4m=0解得m=-1,
∴切线方程为2x-y-1=0,
故选D
点评:本题主要考查了两条直线平行的判定,以及直线的一般式方程,属于基础题.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目