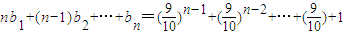题目内容
设向量 ,函数
,函数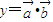 在[0,1]上的最小值与最大值的和为an,又数列{bn}满足:
在[0,1]上的最小值与最大值的和为an,又数列{bn}满足:
(1)求证:an=n+1;
(2)求bn的表达式;
(3)cn=-an•bn,试问数列{cn}中,是否存在正整数k,使得对于任意的正整数n,都有cn≤ck成立?证明你的结论.
【答案】分析:(1)由y=x(x+n)+4x-2=x2+(4+n)x-2在[0,1]上为增函数,知an=n+1
(2)由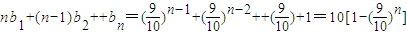
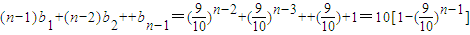 可
可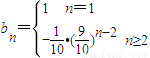
(3)由题意知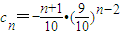 ,
,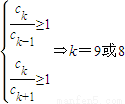 ,由此可知存在k=8,9使得cn≤ck对所有的n∈N*成立
,由此可知存在k=8,9使得cn≤ck对所有的n∈N*成立
解答:解:(1)∵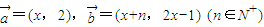 ,
,
∴函数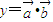 =x(x+n)+4x-2=x2+(4+n)x-2
=x(x+n)+4x-2=x2+(4+n)x-2
判断知,此函数在[0,1]上为增函数,
∴an=-2+1+4+n-2=n+1
(2)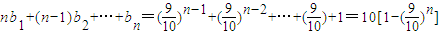
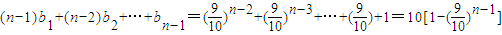
两式相减得: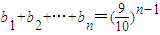
由上式得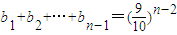
两式作差得
又n=1时,b1=1
所以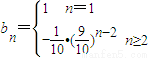
(3)n≥2时,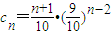 ,
,
令
验证知,当n=1,2也满足
故存在k=8,9使得cn≤ck对所有的n∈N*成立
点评:本题考查数列的性质及其应用,难度较大,解题时要认真审题,仔细解答.
(2)由
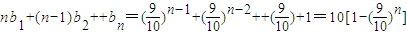
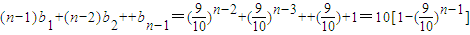 可
可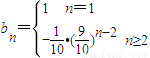
(3)由题意知
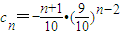 ,
,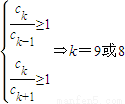 ,由此可知存在k=8,9使得cn≤ck对所有的n∈N*成立
,由此可知存在k=8,9使得cn≤ck对所有的n∈N*成立解答:解:(1)∵
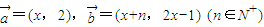 ,
,∴函数
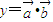 =x(x+n)+4x-2=x2+(4+n)x-2
=x(x+n)+4x-2=x2+(4+n)x-2判断知,此函数在[0,1]上为增函数,
∴an=-2+1+4+n-2=n+1
(2)
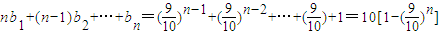
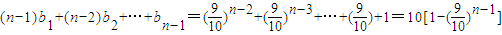
两式相减得:
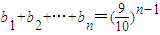
由上式得
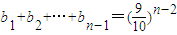
两式作差得

又n=1时,b1=1
所以
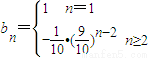
(3)n≥2时,
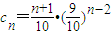 ,
,令

验证知,当n=1,2也满足
故存在k=8,9使得cn≤ck对所有的n∈N*成立
点评:本题考查数列的性质及其应用,难度较大,解题时要认真审题,仔细解答.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
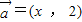 ,
,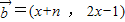 (n为正整数),函数
(n为正整数),函数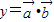 在[0,1]上的最小值与最大值的和为an,又数列{bn}满足:
在[0,1]上的最小值与最大值的和为an,又数列{bn}满足: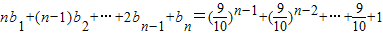 .
.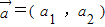 与
与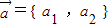 表示意义相同)
表示意义相同)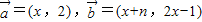 (n∈N*),函数
(n∈N*),函数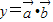 在[0,1]上的最大值与最小值的和为an,又数列{bn}满足:nb1+(n-1)b2+…+2bn-1+bn=
在[0,1]上的最大值与最小值的和为an,又数列{bn}满足:nb1+(n-1)b2+…+2bn-1+bn=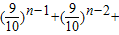
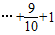 .
.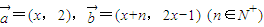 ,函数
,函数 在[0,1]上的最小值与最大值的和为an,又数列{bn}满足:
在[0,1]上的最小值与最大值的和为an,又数列{bn}满足: