题目内容
4．设三棱柱ABC-A1B1C1的侧棱垂直于底面，$AB=AC=2，\;∠\;BAC=90°，\;A{A_1}=2\sqrt{2}$，且三棱柱的所有顶点都在同一球面上，则该球的表面积是16π．分析 根据题意，可将棱柱ABC-A1B1C1补成长方体，长方体的对角线即为球的直径，从而可求球的表面积．
解答 解：∵三棱柱ABC-A1B1C1的侧棱垂直于底面，AB=AC=2，∠BAC=90°，AA1=2$\sqrt{2}$，
∴可将棱柱ABC-AA1B1C1补成长方体，长方体的对角线$\sqrt{4+4+8}$=4，即为球的直径，
∴球的直径为4，
∴球的表面积为4π×22=16π，
故答案为：16π．
点评 本题考查球的表面积，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
在长方形ABCD中，AE=EB，三角形BEF的面积占长方形ABCD面积的$\frac{3}{16}$，那么BF：FC=3：1．
如图，在平面直角坐标系xoy中，椭圆C的标准方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1，直线l与x轴交于点E，与椭圆C交于A，B两点．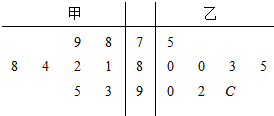
甲、乙两人参加数学竞赛培训，现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次，画出茎叶图如图所示，乙的成绩中有一个数个位数字模糊，在茎叶图中用c表示．（把频率当作概率）