题目内容
已知常数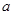 、
、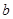 、
、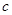 都是实数,函数
都是实数,函数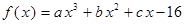 的导函数为
的导函数为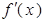 ,
,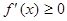 的解集为
的解集为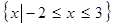 .
.
(Ⅰ)若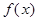 的极大值等于
的极大值等于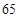 ,求
,求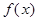 的极小值;
的极小值;
(Ⅱ)设不等式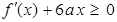 的解集为集合
的解集为集合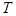 ,当
,当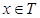 时,函数
时,函数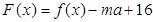 只有一个零点,求实数
只有一个零点,求实数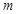 的取值范围.
的取值范围.
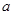 、
、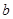 、
、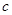 都是实数,函数
都是实数,函数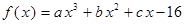 的导函数为
的导函数为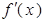 ,
,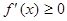 的解集为
的解集为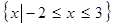 .
.(Ⅰ)若
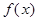 的极大值等于
的极大值等于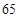 ,求
,求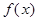 的极小值;
的极小值;(Ⅱ)设不等式
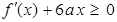 的解集为集合
的解集为集合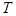 ,当
,当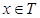 时,函数
时,函数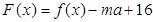 只有一个零点,求实数
只有一个零点,求实数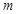 的取值范围.
的取值范围.(Ⅰ) ;(Ⅱ)当
;(Ⅱ)当 或
或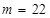 时,函数
时,函数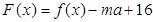 在
在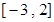 上只有一个零点.
上只有一个零点.
 ;(Ⅱ)当
;(Ⅱ)当 或
或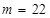 时,函数
时,函数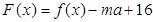 在
在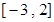 上只有一个零点.
上只有一个零点.试题分析::1.第(Ⅰ)的解答还是要破费周折的.首先要求出导函数
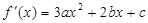 .
.然后根据
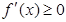 的解集为
的解集为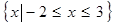 ,通过解混合组,得到
,通过解混合组,得到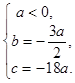 进而得到
进而得到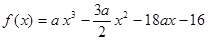 .接下来通过研究函数
.接下来通过研究函数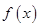 的单调性,由
的单调性,由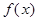 的极大值等于
的极大值等于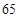 ,可解得
,可解得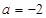 ,这样就可以求出
,这样就可以求出 的极小值
的极小值 .2.第(Ⅱ)问先由不等式
.2.第(Ⅱ)问先由不等式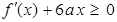 的解集为集合
的解集为集合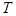 ,可以解得
,可以解得 .然后研究
.然后研究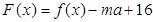 的单调性,值得注意的是
的单调性,值得注意的是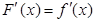 ,换句话说方程两边对
,换句话说方程两边对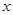 求导数,
求导数, 、
、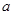 应看作是常数.单调性弄清楚后,还要比较
应看作是常数.单调性弄清楚后,还要比较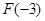 、
、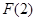 的大小.然后根据
的大小.然后根据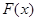 只有一个零点,列出
只有一个零点,列出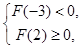 或
或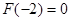 ,最后解之即可.值得注意的是,很多考生漏了
,最后解之即可.值得注意的是,很多考生漏了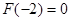 .
.试题解析:(Ⅰ)∵
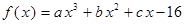 ,∴
,∴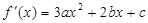 .
. ∵不等式
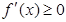 的解集为
的解集为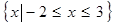 ,
,∴不等式
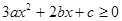 的解集为
的解集为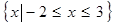 .
.∴
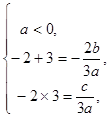 即
即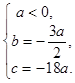
∴
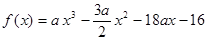 ,
,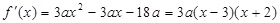 .
.∴当
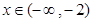 或
或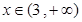 时,
时,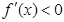 ,即
,即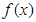 为单调递减函数;
为单调递减函数;当
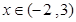 时,
时,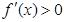 ,即
,即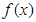 为单调递增函数.
为单调递增函数.∴当
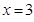 时,
时,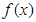 取得极大值,当
取得极大值,当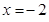 时,
时,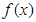 取得极小值.
取得极小值.由已知得
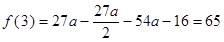 ,解得
,解得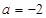 .
. ∴
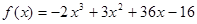 .
.∴
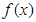 的极小值
的极小值 .
. (Ⅱ)∵
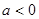 ,
,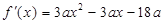 ,
,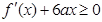 ,
,∴
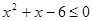 ,解得
,解得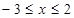 ,即
,即 .
.∵
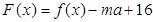 ,∴
,∴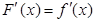 .
.∴当
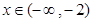 或
或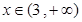 时,
时,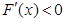 ,即
,即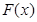 为单调递减函数;
为单调递减函数;当
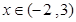 时,
时,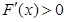 ,即
,即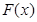 为单调递增函数.
为单调递增函数. ∴当
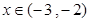 时,
时,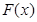 为单调递减函数;
为单调递减函数;当
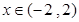 时,
时,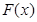 为单调递增函数.
为单调递增函数. ∵
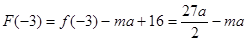 ,
,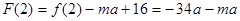 ,
,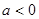 ,
,∴
 .
.∴
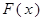 在
在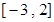 上只有一个零点
上只有一个零点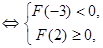 或
或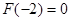 .
.由
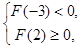 得
得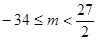 ;
;由
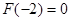 ,即
,即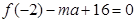 ,得
,得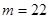 .
.∴实数
 的取值范围为
的取值范围为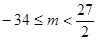 或
或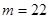 .
. ∴当
 或
或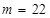 时,函数
时,函数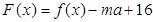 在
在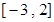 上只有一个零点.
上只有一个零点. 
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
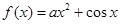 .
.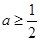 时,函数
时,函数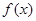 在
在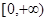 上单调递增;
上单调递增;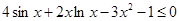 .
.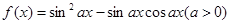 的图象与直线
的图象与直线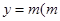 为常数)相切,并且切点的横坐标依次成等差数列,且公差为
为常数)相切,并且切点的横坐标依次成等差数列,且公差为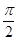
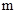 的值;
的值; 是
是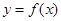 图象的对称中心,且
图象的对称中心,且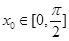 ,求点A的坐标
,求点A的坐标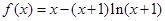 (
(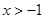 ).
).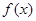 的单调区间;
的单调区间;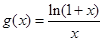 (
(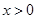 )的单调性证明:当
)的单调性证明:当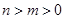 时,
时,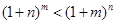 ;
;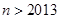 ,且
,且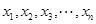 均为正实数,
均为正实数, 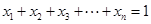 时,
时,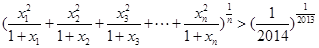 .
.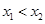 ,求证:
,求证: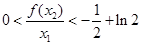 .
.
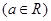 .
. 在
在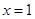 处的切线垂直于直线
处的切线垂直于直线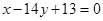 ,求该点的切线方程,并求此时函数
,求该点的切线方程,并求此时函数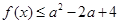 对任意的
对任意的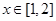 恒成立,求实数
恒成立,求实数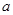 的取值范围.
的取值范围.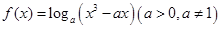 在区间
在区间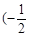 ,0)内单调递增,则
,0)内单调递增,则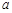 取值范围是( )
取值范围是( )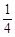 ,1)
,1)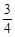 ,1)
,1)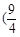 ,
,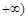
 )
)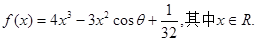
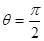 时,判断函数
时,判断函数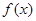 是否有极值;
是否有极值;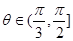 时,
时,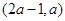 上的增函数,求实数
上的增函数,求实数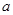 的取值范围.
的取值范围. 