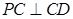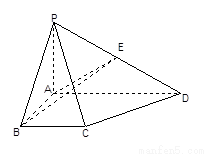题目内容
图形P－ABCD中，底面ABCD是正方形，PA⊥底面ABCD，PA＝AB，Q是PC中点．AC，BD交于O点．
（1）二面角Q－BD－C的大小：
（2）求二面角B－QD－C的大小．
【答案】
（1）
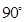（2）
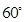
【解析】
试题分析：连QO，则QO∥PA且QO＝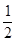
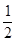PA＝AB
∵ PA⊥面ABCD
∴ QO⊥面ABCD
面QBD过QO，
∴ 面QBD⊥面ABCD
故二面角Q－BD－C等于90°．
（Ⅱ）解：过O作OH⊥QD，垂足为H，连CH．
∵ 面QBD⊥面BCD，
又∵ CO⊥BD
CO⊥面QBD
CH在面QBD内的射影是OH
∵ OH⊥QD
∴ CH⊥QD
于是∠OHC是二面角的平面角．
设正方形ABCD边长2，
则OQ＝1，O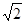D＝
，QD＝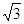
．
∵ OH·QD＝OQ·OD
∴ OH＝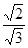
．
又OC＝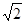
在Rt△COH中：tan∠OHC＝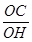
＝·＝
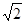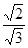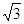
∴ ∠OHC＝60°
故二面角B－QD－C等于60°．
考点：二面角求解
点评：本题还可用空间向量的方法求二面角
练习册系列答案
阅读快车系列答案
相关题目
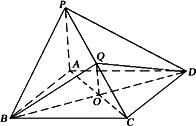
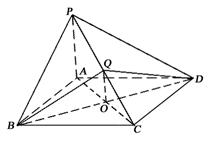AC，BD交于O点．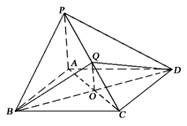
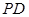边的中点，且PA⊥底面ABCD。
