题目内容
(本题满分12分)
在立体图形P-ABCD中,底面ABCD是一个直角梯形,∠BAD=90°,AD∥BC,
AB=BC=a,AD=PA=2a,E是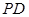 边的中点,且PA⊥底面ABCD。
边的中点,且PA⊥底面ABCD。
(1)求证:BE⊥PD
(2)求证: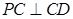
(3)求异面直线AE与CD所成的角.
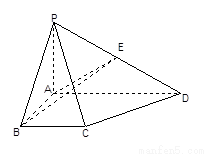
【答案】
(1)略
(2)略
(3)异面直线AE与CD所成的角为
【解析】证明:(1) PA⊥底面ABCD
PA⊥底面ABCD 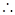
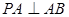
又 ∠BAD=90°
∠BAD=90° 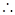
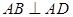
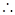
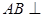 平面
平面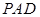
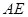 是斜线
是斜线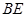 在平面
在平面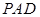 内的射影
内的射影
 AE⊥PD
AE⊥PD 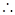 BE⊥PD
BE⊥PD
(2)连结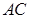
 PA⊥底面ABCD
PA⊥底面ABCD 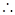
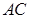 是斜线
是斜线 在平面
在平面 内的射影
内的射影

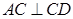
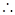
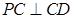
(3)过 点作
点作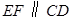 交
交 于
于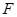 ,连结
,连结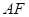 ,则
,则 (或其补角)为异面直线AE与CD所成的角。由(2)知
(或其补角)为异面直线AE与CD所成的角。由(2)知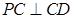

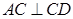
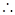
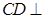 平面
平面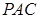
又
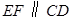
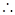
 平面
平面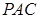
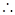

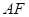
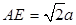
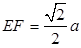
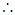
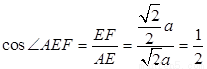
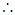
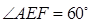
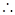 异面直线AE与CD所成的角为
异面直线AE与CD所成的角为

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面