题目内容
已知双曲线的两条渐近线的夹角为60°,则其离心率为
2或
2
| ||
| 3 |
2或
.2
| ||
| 3 |
分析:先由双曲线的两条渐近线的夹角为60°,得双曲线的两条渐近线的斜率±
或±
,由于不知双曲线的焦点位置,故通过讨论分别计算离心率,由
=
或
=
,再由双曲线中c2=a2+b2,求其离心率即可
| 3 |
| ||
| 3 |
| b |
| a |
| ||
| 3 |
| a |
| b |
| ||
| 3 |
解答:解:∵双曲线的两条渐近线的夹角为60°,且渐近线关于x、y轴对称,
若夹角在x轴上,则双曲线的两条渐近线的倾斜角为30°,150°,斜率为±
若夹角在y轴上,则双曲线的两条渐近线的倾斜角为60°,120°,斜率为±
①若双曲线的焦点在x轴上,则
=
或
=
∵c2=a2+b2
∴
=
或
=3
∴e2-1=
或e2-1=3
∴e=
或e=2
②若双曲线的焦点在y轴上,则
=
或
=
∵c2=a2+b2
∴
=
或
=3
∴e2-1=
或e2-1=3
∴e=
或e=2
综上所述,离心率为2或
故答案为 2或
若夹角在x轴上,则双曲线的两条渐近线的倾斜角为30°,150°,斜率为±
| ||
| 3 |
若夹角在y轴上,则双曲线的两条渐近线的倾斜角为60°,120°,斜率为±
| 3 |
①若双曲线的焦点在x轴上,则
| b |
| a |
| ||
| 3 |
| b |
| a |
| 3 |
∵c2=a2+b2
∴
| c2-a2 |
| a2 |
| 1 |
| 3 |
| c2-a2 |
| a2 |
∴e2-1=
| 1 |
| 3 |
∴e=
2
| ||
| 3 |
②若双曲线的焦点在y轴上,则
| a |
| b |
| ||
| 3 |
| a |
| b |
| 3 |
∵c2=a2+b2
∴
| a2 |
| c2-a2 |
| 1 |
| 3 |
| a2 |
| c2-a2 |
∴e2-1=
| 1 |
| 3 |
∴e=
2
| ||
| 3 |
综上所述,离心率为2或
2
| ||
| 3 |
故答案为 2或
2
| ||
| 3 |
点评:本题考查了双曲线的几何性质,由渐近线的斜率推导双曲线的离心率是解决本题的关键

练习册系列答案
相关题目
 ,0)为右焦点的双曲线C的离心率,
,0)为右焦点的双曲线C的离心率,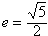 。
。