题目内容
已知⊙O的方程为x2+y2=1,则⊙O上的点到直线
(t为参数)的距离的最大值为______.
|
∵直线
(t为参数)
∴3x+4y=10,
∵⊙O的方程为x2+y2=1,圆心为(0,0),
设直线3x+4y=k与圆相切,
∴
=1,
∴k=±5,
∴直线3x+4y=k与3x+4y=10,之间的距离就是⊙O上的点到直线的距离的最大值,
∴d=
,
∴d的最大值是
=3,
故答案为:3.
|
∴3x+4y=10,
∵⊙O的方程为x2+y2=1,圆心为(0,0),
设直线3x+4y=k与圆相切,
∴
| |k| |
| 5 |
∴k=±5,
∴直线3x+4y=k与3x+4y=10,之间的距离就是⊙O上的点到直线的距离的最大值,
∴d=
| |10±5| |
| 5 |
∴d的最大值是
| 15 |
| 5 |
故答案为:3.

练习册系列答案
相关题目






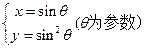 与直线
与直线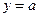 有两个公共点,则实数
有两个公共点,则实数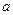 的取值范围是_________________.
的取值范围是_________________.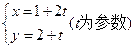 被圆
被圆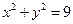 截得的弦长为( )
截得的弦长为( )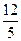
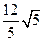
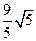
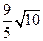
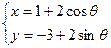 化成普通方程是______________________.
化成普通方程是______________________.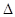
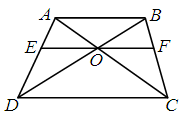
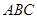 中
中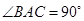 ,
,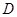 是
是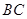 边的中点,
边的中点,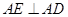 ,
,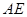 交
交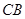 的延长 线于
的延长 线于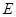 , 则下面结论中正确的是
, 则下面结论中正确的是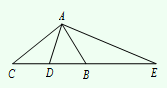
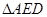 ∽
∽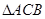
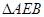 ∽
∽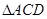
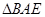 ∽
∽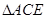
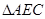 ∽
∽