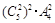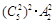题目内容
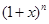 的展开式中,
的展开式中,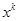 的系数可以表示从
的系数可以表示从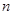 个不同物体中选出
个不同物体中选出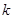 个的方法总数.下列各式的展开式中
个的方法总数.下列各式的展开式中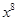 的系数恰能表示从重量分别为
的系数恰能表示从重量分别为 克的砝码(每种砝码各一个)中选出若干个,使其总重量恰为
克的砝码(每种砝码各一个)中选出若干个,使其总重量恰为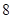 克的方法总数的选项是()
克的方法总数的选项是()
A.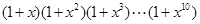 |
B. |
C.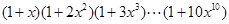 |
D.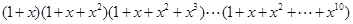 |
A
解析试题分析:对于这10个砝码而言,只有选与不选的区别。
对于重量为n的砝码,选择了它,则它对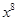 中的指数8的贡献为n,在代数式中即为
中的指数8的贡献为n,在代数式中即为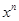 ;
;
如果没有选择该砝码,则它对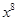 中的指数8的贡献为0,在代数式中即为
中的指数8的贡献为0,在代数式中即为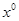 =1,
=1,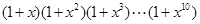 可以看成(
可以看成(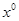 +x)(
+x)(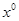 +
+ )(
)(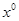 +
+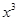 )灬(
)灬(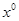 +
+ ),在上述的代数式子相乘的过程中即为从每个独立的代数式
),在上述的代数式子相乘的过程中即为从每个独立的代数式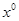 +
+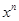 中的2个项任意选择一个相乘(选择一个就是代表每个砝码的选择与否),最后将这些相乘的结果相加合并同类项,在每个独立的代数式
中的2个项任意选择一个相乘(选择一个就是代表每个砝码的选择与否),最后将这些相乘的结果相加合并同类项,在每个独立的代数式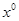 +
+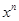 中的2个项任意选择一个相乘的过程中如果得到
中的2个项任意选择一个相乘的过程中如果得到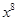 ,则这就是一种总重量恰为8克的方法,故选A。
,则这就是一种总重量恰为8克的方法,故选A。
考点:组合数公式,组合的应用。
点评:中档题,关键是将问题加以转化,转化成二项式的展开问题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若 =
=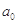 +
+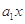 +
+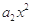 +…+
+…+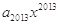 (x∈R),则
(x∈R),则 +
+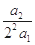 +
+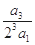 +…+
+…+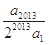
A.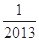 | B.-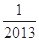 | C.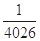 | D.-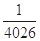 |
已知 的展开式的二项式系数之和为32,则展开式中含
的展开式的二项式系数之和为32,则展开式中含 项的系数是( )
项的系数是( )
| A.5 | B.20 | C.10 | D.40 |
给一个正方体的六个面涂上四种不同颜色(红、黄、绿、蓝),要求相邻两个面涂不同的颜色,则共有涂色方法( )(涂色后,任意翻转正方体,能使正方体各面颜色一致,我们认为是同一种涂色方法)
| A.6种 | B.12种 | C.24种 | D.48种 |
设 ,
, ,
,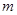 为整数(
为整数( ),若
),若 和
和 被
被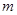 除得的余数相同,则称
除得的余数相同,则称 和
和 对模
对模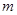 同余,记作
同余,记作 ,已知
,已知 ,且
,且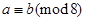 ,则
,则 的值可为( ).
的值可为( ).
| A.2011 | B.2012 | C.2009 | D.2010 |
男女生共8人,从中任选3人,出现2个男生,1个女生的概率为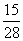 ,则其中女生人数是
,则其中女生人数是
| A.2人 | B.3人 | C.4人 | D.2人或3人 |
从0,1,2,3,4,5六个数中任取四个互异的数字组成四位数,个位,百位上必排偶数数字的四位数共有( )
| A.52个 | B.60个 | C.54 | D.66个 |
 种
种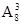 种
种  种
种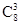 种
种