Question

【题目】已知椭圆C： =1（a＞b＞0）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形．
（Ⅰ）求椭圆C的标准方程和长轴长；
（Ⅱ）设F为椭圆C的左焦点，P为直线x=﹣3上任意一点，过点F作直线PF的垂线交椭圆C于M，N，记d1 ， d2分别为点M和N到直线OP的距离，证明：d1=d2 ．

Answer 1

【答案】解：（Ⅰ）由题意可知椭圆的焦点在x轴上，2c=4，c=2， =2b，
由a2=b2+c2 ， 解得a2=6，b2=2，
∴椭圆C的标准方程为 ，椭圆C的长轴长为 ．
（Ⅱ）由（Ⅰ）可知点F的坐标为（﹣2，0），设点P的坐标为（﹣3，m），
则直线PF的斜率 ，
当m≠0时，直线MN的斜率 ，直线MN的方程是x=my﹣2，
当m=0时，直线MN的方程是x=﹣2，也符合x=my﹣2的形式，
设M（x1 ， y1），N（x2 ， y2），将直线MN的方程与椭圆C的方程联立，
得 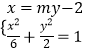，消去x，得（m2+3）y2﹣4my﹣2=0，
其判别式△=16m2+8（m2+3）＞0，
所以 ， ， ，
设T为线段MN的中点，则点T的坐标为 ，
所以直线OT的斜率 ，
又直线OP的斜率 ，
所以点T在直线OP上，
由三角形全等的判定和性质可知：d1=d2
【解析】（Ⅰ）由椭圆的性质可知：c=2， =2b，即可求得a和b的值，求得椭圆方程；（Ⅱ）由（Ⅰ）求得直线MN的方程，代入椭圆方程，由韦达定理及中点坐标公式可知求得MN的中点T，由kOT=kOP ， 由三角形全等的判定和性质可知：d1=d2 ．
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：，焦点在y轴：．