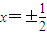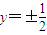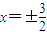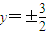题目内容
双曲线的两条渐进线方程分别为x-
y=0和x+
y=0,双曲线上的点满足不等式x2-3y2<0,已知双曲线的焦距为4,则双曲线的准线方程为( )
| 3 |
| 3 |
分析:先根据双曲线上的点满足不等式x2-3y2<0,得出双曲线焦点所在的坐标轴,再设出双曲线的标准方程,进而根据渐近线方程和焦距联立方程求得a和b,答案可得.
解答: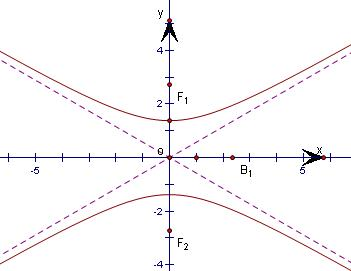 解:不等式x2-3y2<0即(x-
解:不等式x2-3y2<0即(x-
y)(x+
y)<0,此不等式表示的平面区域为双曲线的两条渐近线x-
y=0和x+
y=0相交所成的上下的对角区域.
∴双曲线的焦点必在y轴上,
∵当双曲线焦点在y轴上时,渐近线方程为y=±
x,
所以
=
,又2c=4,且a2+b2=c2,
联立解得a=1,b=
.
则双曲线的准线方程为:y=±
即y=±
故选C.
 解:不等式x2-3y2<0即(x-
解:不等式x2-3y2<0即(x-| 3 |
| 3 |
| 3 |
| 3 |
∴双曲线的焦点必在y轴上,
∵当双曲线焦点在y轴上时,渐近线方程为y=±
| a |
| b |
所以
| a |
| b |
| 1 | ||
|
联立解得a=1,b=
| 3 |
则双曲线的准线方程为:y=±
| a2 |
| c |
| 1 |
| 2 |
故选C.
点评:本题主要考查了双曲线的标准方程、二元一次不等式表示的平面区域等基本知识.属基础题.

练习册系列答案
相关题目
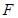 为椭圆
为椭圆
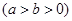 的右焦点,直线
的右焦点,直线 过点
过点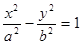 的两条渐进线
的两条渐进线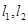 分别交于点
分别交于点 ,与椭圆交于点
,与椭圆交于点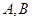 .
.
 ,双曲线的焦距为4。求椭圆方程。
,双曲线的焦距为4。求椭圆方程。 (
( 为坐标原点),
为坐标原点), ,求椭圆的离心率
,求椭圆的离心率
 y=0和x+
y=0和x+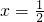
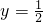
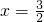
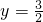
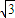 y=0和x+
y=0和x+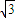 y=0,双曲线上的点满足不等式x2-3y2<0,已知双曲线的焦距为4,则双曲线的准线方程为( )
y=0,双曲线上的点满足不等式x2-3y2<0,已知双曲线的焦距为4,则双曲线的准线方程为( )