题目内容
若第一象限内的点A(x、y)落在经过点(6,-2)且具有方向向量
=(1,-
)的直线上,则log
x+log
y有( )
| e |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
A、最大值
| ||
| B、最大值1 | ||
C、最小值
| ||
| D、最小值1 |
分析:先根据直线的点斜式方程求出A点坐标满足的关系式,代入log
x+log
y,再由二次函数求最值的方法求出最大值即可.
| 3 |
| 2 |
| 3 |
| 2 |
解答:解:∵点A(x、y)所在直线的方向向量为
=(1,-
),∴k=-
又∵直线经过点(6,-2),∴点A(x、y)满足y+2=-
(x-6),即y=-
x+2,
∴log
x+log
y=log
xy=log
x(-
x+2)=log
-
(x2-3x)
可知,当x=
时,上式有最大值为log
-
((
)2-3 ×
)=1
故选B
| e |
| 2 |
| 3 |
| 2 |
| 3 |
又∵直线经过点(6,-2),∴点A(x、y)满足y+2=-
| 2 |
| 3 |
| 2 |
| 3 |
∴log
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
可知,当x=
| 3 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
故选B
点评:本题主要考查了直线方程与二次函数现结合求最值,属于基础题.

练习册系列答案
相关题目
若第一象限内的点A(x,y)落在经过点(6,-2)且方向向量为
=(3,-2)的直线l上,则t=log
y-log
x有( )
| a |
| 3 |
| 2 |
| 2 |
| 3 |
| A、最大值1 | ||
B、最大值
| ||
C、最小值
| ||
| D、最小值1 |
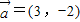 的直线l上,则t=
的直线l上,则t=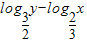 有( )
有( )

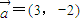 的直线l上,则t=
的直线l上,则t=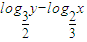 有( )
有( )
