题目内容
若第一象限内的点A(x,y)落在经过点(6,-2)且具有方向向量
=(3,-2)的直线l上,则log
x+log
y有( )
| e |
| 3 |
| 2 |
| 3 |
| 2 |
分析:由向量平行可得2x+3y=6,而所求=log
•2x•3y,由基本不等式可得.
| 3 |
| 2 |
| 1 |
| 6 |
解答:解:由题意可得向量(x-6,y+2)与向量
=(3,-2)平行,
故可得3(y+2)-(-2)(x-6)=0,即2x+3y=6,x,y为正数,
故log
x+log
y=log
xy=log
•2x•3y≤log
•(
)2=1
当且仅当2x=3y,即x=
,y=1时取等号,
故则log
x+log
y有最大值1
故选B
| e |
故可得3(y+2)-(-2)(x-6)=0,即2x+3y=6,x,y为正数,
故log
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 6 |
| 3 |
| 2 |
| 1 |
| 6 |
| 2x+3y |
| 2 |
当且仅当2x=3y,即x=
| 3 |
| 2 |
故则log
| 3 |
| 2 |
| 3 |
| 2 |
故选B
点评:本题考查平面向量的坐标运算,涉及直线的方向向量和基本不等式的应用,属中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
若第一象限内的点A(x,y)落在经过点(6,-2)且方向向量为
=(3,-2)的直线l上,则t=log
y-log
x有( )
| a |
| 3 |
| 2 |
| 2 |
| 3 |
| A、最大值1 | ||
B、最大值
| ||
C、最小值
| ||
| D、最小值1 |
若第一象限内的点A(x、y)落在经过点(6,-2)且具有方向向量
=(1,-
)的直线上,则log
x+log
y有( )
| e |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
A、最大值
| ||
| B、最大值1 | ||
C、最小值
| ||
| D、最小值1 |
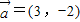 的直线l上,则t=
的直线l上,则t=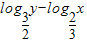 有( )
有( )

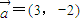 的直线l上,则t=
的直线l上,则t=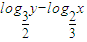 有( )
有( )
