题目内容
.(12分)如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.
(1)求证:B1B∥平面D1AC;
(2)求证:平面D1AC⊥平面B1BDD1.
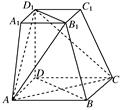
(1)求证:B1B∥平面D1AC;
(2)求证:平面D1AC⊥平面B1BDD1.

证明: (1)设AC∩BD=E,连结D1E,
∵平面ABCD∥平面A1B1C1D1.
∴B1D1∥BE,∵B1D1=BE=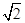 ,
,
∴四边形B1D1EB是平行四边形,
所以B1B∥D1E.
又因为B1B?平面D1AC,D1E?平面D1AC,
所以B1B∥平面D1AC ---------------------------------------6分
(2)证明:侧棱DD1⊥平面ABCD,AC?平面ABCD,
∴AC⊥DD1.
∵下底ABCD是正方形,AC⊥BD.
∵DD1与DB是平面B1BDD1内的两条相交直线,
∴AC⊥平面B1BDD1
∵AC?平面D1AC,∴平面D1AC⊥平面B1BDD1.---------------------12分
∵平面ABCD∥平面A1B1C1D1.
∴B1D1∥BE,∵B1D1=BE=
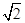 ,
,∴四边形B1D1EB是平行四边形,
所以B1B∥D1E.
又因为B1B?平面D1AC,D1E?平面D1AC,
所以B1B∥平面D1AC ---------------------------------------6分
(2)证明:侧棱DD1⊥平面ABCD,AC?平面ABCD,
∴AC⊥DD1.
∵下底ABCD是正方形,AC⊥BD.
∵DD1与DB是平面B1BDD1内的两条相交直线,
∴AC⊥平面B1BDD1
∵AC?平面D1AC,∴平面D1AC⊥平面B1BDD1.---------------------12分
略

练习册系列答案
相关题目
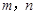 是两条不同直线,
是两条不同直线,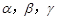 是三个不同平面,正确命题的个数是( )
是三个不同平面,正确命题的个数是( )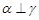 ,
,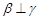 ,则
,则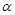 //
//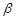 ②若
②若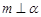 ,
,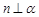 ,则
,则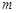 //
//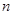
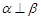 ,
,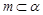 ,则
,则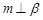 ④若
④若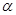 ,
,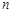 //
//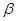 ,则
,则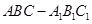 中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点
中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点
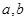 为两条直线,
为两条直线,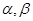 为两个平面,下列四个命题中,真命题为( )
为两个平面,下列四个命题中,真命题为( ) 所成角相等,则
所成角相等,则
 ,则
,则 ,则
,则
 ,则
,则
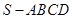 中,
中,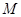 是
是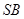 的中点,
的中点,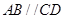 ,
,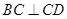 ,且
,且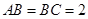 ,
,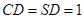 ,又
,又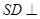 面
面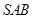 .
.
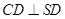 ;
;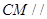 面
面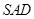 ;
;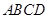 中,对角线
中,对角线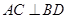 ,且
,且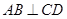 ,则点
,则点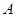 在
在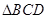 内的射影
内的射影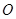 是
是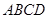 为平行四边形,
为平行四边形,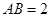 ,
,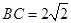 ,
,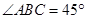 ,
,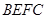 是长方形,
是长方形,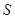 是
是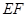 的中点,
的中点,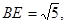 平面
平面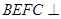 平面
平面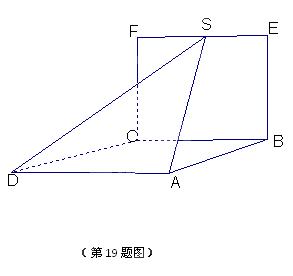
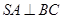 ;
;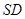 与平面
与平面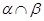 =EF,AB
=EF,AB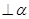 ,CD
,CD
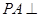 圆
圆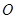 所在平面,
所在平面,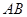 是圆
是圆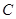 是圆
是圆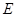 、
、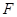 分别是点
分别是点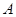 在
在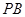 、
、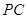 上的射影,给出下列结论:①
上的射影,给出下列结论:①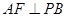 ;②
;②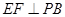 ;③
;③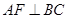 ;④
;④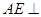 平面
平面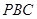 ,其中正确的结论是____________。
,其中正确的结论是____________。