题目内容
8、如图，设平面α∩β=EF，AB⊥α，CD⊥α，垂足分别为B，D，且AB≠CD．如果增加一个条件就能推出BD⊥EF，给出四个条件：①AC⊥β；②AC⊥EF；③AC与BD在β内的正投影在同一条直线上；④AC与BD在平面β内的正投影所在的直线交于一点．那么这个条件不可能是（ ）分析：逐一判定，（1）∵EF⊥AC；EF⊥AB说明EF⊥面ACDB（2）同（1）；
（3）由三垂线定理可知EF⊥AC；EF⊥AB说明EF⊥面ACDB；（4）不正确是显然的，容易推出矛盾结果．
（3）由三垂线定理可知EF⊥AC；EF⊥AB说明EF⊥面ACDB；（4）不正确是显然的，容易推出矛盾结果．
解答：解：（1）、（2）都能说明EF⊥面ACDB；即都能说明EF垂直平面ACBD中的两条相交直线AC、BD；（3）（3）由三垂线定理可知EF⊥AC；EF⊥AB说明EF⊥面ACDB；（（4）说明AC、BD 中的两条直线都不垂直EF．否则两条直线重合．
故选D．
故选D．
点评：本题考查空间直线与平面之间的位置关系，线面垂直和射影等知识，是基础题．
练习册系列答案
相关题目
15、如图，设平面α∩β=EF，AB⊥α，CD⊥α，垂足分别为B，D，若增加一个条件，就能推出BD⊥EF，现有：①AC⊥β；②AC与α，β所成的角相等；③AC与CD在β内的射影在同一条直线上；④AC∥EF，那么上述几个条件中能成为增加的条件的序号是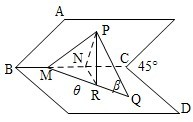
如图，设平面AC和BD相交于BC，它们所成的一个二面角为45°，P为平面AC内的一点，Q为面BD内的一点，已知直线MQ是直线PQ在平面BD内的射影，并且M在BC上又设PQ与平面BD所成的角为β，∠CMQ=θ（0°＜θ＜90°），线段PM的长为a，求线段PQ的长．
（2009•中山模拟）如图，设平面α∩β=EF，AB⊥α，CD⊥α，垂足．分别为B，D，若增加一个条件，就能推出BD⊥EF．现有①AC⊥β；②AC与α，β所成的角相等；③AC与CD在β内的射影在同一条直线上；④AC∥EF．那么上述几个条件中能成为增加条件的个数是（ ）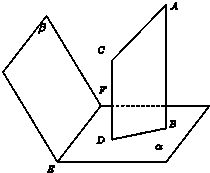
如图，设平面α∩β=EFAB⊥α，CD⊥α垂足分别为B，D，且AB≠CD．如果增加一个条件就能推出BD⊥EF，给出四个条件：