题目内容
若长方体从一顶点出发的三条棱长之比为1：2：3，对角线长为
，则它的体积为
；
．
| ||
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
分析：连接底面对角线，底面对角线的平方是底面长和宽的平方和，体对角线的平方等于面对角线的平方加上高的平方，直接计算即可．
解答：解：因为在长方体中，底面对角线的平方是底面长和宽的平方和，
体对角线的平方等于面对角线的平方加上高的平方；
设三条棱长k，2k，3k，长方体对角线的长：
=
，
解得k=
，
∴该长方体的体积v=
×1×
=
．
故答案为：
．
体对角线的平方等于面对角线的平方加上高的平方；
设三条棱长k，2k，3k，长方体对角线的长：
| k2+4k2+9k2 |
| ||
| 2 |
解得k=
| 1 |
| 2 |
∴该长方体的体积v=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
故答案为：
| 3 |
| 4 |
点评：本题考查长方体的体积，解题时要认真审题，注意长方体对角线的求法，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
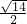，则它的体积为________；________．