题目内容
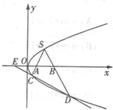 如图,S(1,1)是抛物线为y2=2px(p>0)上的一点,弦SC,SD分别交x小轴于A,B两点,且SA=SB.
如图,S(1,1)是抛物线为y2=2px(p>0)上的一点,弦SC,SD分别交x小轴于A,B两点,且SA=SB.(I)求证:直线CD的斜率为定值;
(Ⅱ)延长DC交x轴于点E,若
| EC |
| 1 |
| 3 |
| ED |
分析:(1)将点(1,1)代入y2=2px,得2p=1,抛物线方程为y2=x,设直线SA的方程为y-1=k(x-1),C(x1,y1),与抛物线方程y2=x联立得:ky2-y+1-k=0.再由根与系数的关系能够导出直线CD的斜率为定值.
(2)设E(t,0),由
=
,知(
-t,
-1)=
(
-t,
-1),解得k=2,所以直线SA的方程为y=2x-1,由此能求出cos∠CSD=cos∠ASB的值.
(2)设E(t,0),由
| EC |
| 1 |
| 3 |
| ED |
| (1-k)2 |
| k2 |
| 1 |
| k |
| 1 |
| 3 |
| (1+k)2 |
| k2 |
| 1 |
| k |
解答:解:(1)将点(1,1)代入y2=2px,得2p=1
∴抛物线方程为y2=x(1分)
设直线SA的方程为y-1=k(x-1),C(x1,y1)
与抛物线方程y2=x联立得:ky2-y+1-k=0(2分)
∴y1+1=
∴y1=
-1
C(
,
-1)(3分)
由题意有SA=SB,∴直线SB的斜率为-k
∴D(
,-
-1)(4分)
∴KCD=
=-
(5分)
(2)设E(t,0)
∵
=
∴(
-t,
-1)=
(
-t,
-1)
-1=
(-
-1)(6分)
∴k=2(7分)
∴直线SA的方程为y=2x-1(8分)
B(
,0)∴A(
,0)(9分)
同理(10分)
∴cos∠CSD=cos∠ASB=
=
.(12分)
∴抛物线方程为y2=x(1分)
设直线SA的方程为y-1=k(x-1),C(x1,y1)
与抛物线方程y2=x联立得:ky2-y+1-k=0(2分)
∴y1+1=
| 1 |
| k |
| 1 |
| k |
C(
| (1-k)2 |
| k2 |
| 1 |
| k |
由题意有SA=SB,∴直线SB的斜率为-k
∴D(
| (1+k)2 |
| k2 |
| 1 |
| k |
∴KCD=
| ||||
|
| 1 |
| 2 |
(2)设E(t,0)
∵
| EC |
| 1 |
| 3 |
| ED |
∴(
| (1-k)2 |
| k2 |
| 1 |
| k |
| 1 |
| 3 |
| (1+k)2 |
| k2 |
| 1 |
| k |
| 1 |
| k |
| 1 |
| 3 |
| 1 |
| k |
∴k=2(7分)
∴直线SA的方程为y=2x-1(8分)
B(
| 3 |
| 2 |
| 1 |
| 2 |
同理(10分)
∴cos∠CSD=cos∠ASB=
| SA2+SB2-AB2 |
| 2SB•SA |
| 3 |
| 5 |
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,注意公式的合理运用.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 如图,S(1,1)是抛物线为y2=2px(p>0)上的一点,弦SC,SD分别交x轴于A,B两点,且SA=SB.
如图,S(1,1)是抛物线为y2=2px(p>0)上的一点,弦SC,SD分别交x轴于A,B两点,且SA=SB. |DE|,求cos2∠CSD的值.
|DE|,求cos2∠CSD的值.
 ,求cos∠CSD的值.
,求cos∠CSD的值.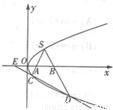
 ,求cos∠CSD的值.
,求cos∠CSD的值.