题目内容
实数a,b满足0<a<b<1,则下列不等式正确的是( )A.ab<ba
B.a-b<b-b
C.a-a<b-b
D.bb<ab
【答案】分析:选项A可由指数函数y=ax和幂函数y=xa的单调性可得;选项BD均可由幂函数的单调性推翻,而选项C可举特值证明a-a>b-b,从而可得答案.
解答:解:选项A,由指数函数y=ax单调递减可得ab<aa,
再由幂函数y=xa单调递增可得aa<ab,故可得ab<ba,A正确;
选项B,由幂函数y=x-b在(0,1)单调递减,可推出a-b>b-b,故B错误;
选项C,可取a= ,b=
,b= ,可得a-a=
,可得a-a=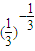 =
= =
=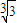 =
=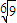 ,b-b=
,b-b=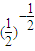 =
=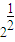 =
=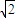 =
=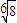 ,
,
显然有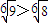 ,即a-a>b-b,故C错误;
,即a-a>b-b,故C错误;
选项D,由幂函数y=xb在(0,1)单调递增,可推出ab<bb,故D错误;
故选A
点评:本题考查不等关系和不等式,涉及幂函数指数函数的单调性,属基础题.
解答:解:选项A,由指数函数y=ax单调递减可得ab<aa,
再由幂函数y=xa单调递增可得aa<ab,故可得ab<ba,A正确;
选项B,由幂函数y=x-b在(0,1)单调递减,可推出a-b>b-b,故B错误;
选项C,可取a=
 ,b=
,b= ,可得a-a=
,可得a-a=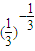 =
= =
=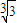 =
=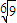 ,b-b=
,b-b=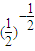 =
=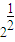 =
=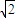 =
=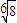 ,
,显然有
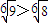 ,即a-a>b-b,故C错误;
,即a-a>b-b,故C错误;选项D,由幂函数y=xb在(0,1)单调递增,可推出ab<bb,故D错误;
故选A
点评:本题考查不等关系和不等式,涉及幂函数指数函数的单调性,属基础题.

练习册系列答案
相关题目
若实数a,b满足0<a<b,且a+b=1.则下列四个数中最大的是( )
A、
| ||
| B、a2+b2 | ||
| C、2ab | ||
| D、a |