题目内容
下列命题中,假命题的个数为
①对所有正数P,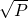 <P;
<P;
②不存在实数x,使x<4且x2+5x=24;
③存在实数x,使得-1≤x+≤1且x2>4;
④3>3.
- A.1
- B.2
- C.3
- D.4
D
分析:对于①,通过举例说明该命题为假命题;
对于②,直接求解二次方程的根即可说明命题是假命题;
对于③,由两个不等式的解集为空集,说明命题是假命题;
对于④,该不等式显然不成立.
由以上分析即可得到答案.
解答:取p=0.01,则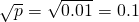 ,
, ,∴①为假命题;
,∴①为假命题;
由x2+5x=24,解得:x=-8或x=3,∴存在实数x=-8或x=3,满足x<4且x2+5x=24,∴②为假命题;
由-1≤x+1≤1,得:-2≤x≤0,由x2>4,得:x<-2或x>2,
∴不存在实数x,使得-1≤x+≤1且x2>4,∴③为假命题;
3>3显然错误,∴④为假命题.
所以,给出的四个命题均为假命题.
故选D.
点评:本题考查了命题的真真假判断与应用,判断一个命题为真命题,需要严格的理论证明,说明一个命题为假命题,只需举一反例即可,此题是基础题.
分析:对于①,通过举例说明该命题为假命题;
对于②,直接求解二次方程的根即可说明命题是假命题;
对于③,由两个不等式的解集为空集,说明命题是假命题;
对于④,该不等式显然不成立.
由以上分析即可得到答案.
解答:取p=0.01,则
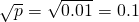 ,
, ,∴①为假命题;
,∴①为假命题;由x2+5x=24,解得:x=-8或x=3,∴存在实数x=-8或x=3,满足x<4且x2+5x=24,∴②为假命题;
由-1≤x+1≤1,得:-2≤x≤0,由x2>4,得:x<-2或x>2,
∴不存在实数x,使得-1≤x+≤1且x2>4,∴③为假命题;
3>3显然错误,∴④为假命题.
所以,给出的四个命题均为假命题.
故选D.
点评:本题考查了命题的真真假判断与应用,判断一个命题为真命题,需要严格的理论证明,说明一个命题为假命题,只需举一反例即可,此题是基础题.

练习册系列答案
相关题目

 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充要条件
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充要条件