题目内容
函数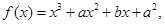 在
在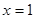 时有极值
时有极值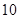 ,那么
,那么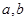 的值分别为____。
的值分别为____。
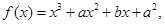 在
在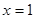 时有极值
时有极值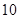 ,那么
,那么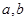 的值分别为____。
的值分别为____。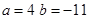
解:∵f(x)=x3+ax2+bx+a2,∴f′(x)=3x2+2ax+b,
∴f′(1)=2a+b+3=0,f(1)=a2+a+b+1=10 ∴2a+b=-3a 2+a+b=9,
所以a=-3,b=3,或a=4,b=-11, 当a=-3时,f′(x)=3x2-6x+3=3(x-1)2≥0,
∴x=1不是极值点 故答案为:4,-11.
∴f′(1)=2a+b+3=0,f(1)=a2+a+b+1=10 ∴2a+b=-3a 2+a+b=9,
所以a=-3,b=3,或a=4,b=-11, 当a=-3时,f′(x)=3x2-6x+3=3(x-1)2≥0,
∴x=1不是极值点 故答案为:4,-11.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
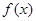 是定义在
是定义在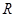 上的可导函数,且满足
上的可导函数,且满足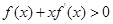 .则不等式
.则不等式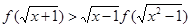 的解集为 .
的解集为 .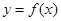 的图象如图所示,若
的图象如图所示,若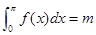 ,则
,则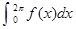 等于( )
等于( )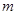
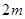
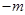
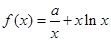 ,
, 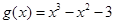 .
.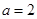 时,求曲线
时,求曲线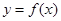 在
在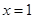 处的切线方程;
处的切线方程;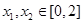 ,使得
,使得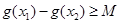 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数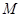 ;
;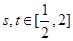 ,都有
,都有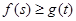 成立,求实数
成立,求实数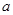 的取值范围.
的取值范围.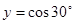 , 则导数
, 则导数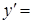 ( )
( ) 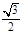
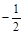
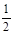
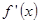 是函数
是函数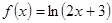 的导函数,则
的导函数,则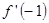 的值为 ( )
的值为 ( )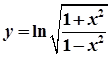 的导数为 。
的导数为 。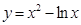 上的任意一点,则点P到直线
上的任意一点,则点P到直线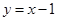 的最小距离为 ▲
的最小距离为 ▲