题目内容
若复数z=cosθ+isinθ且z2+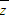
2=1，则sin2θ=（ ）A．
B．
C．
D．-
【答案】分析：先根据题目所给复数的条件写出三角函数关系式，逆用余弦的二倍角公式，再变形用余弦的二倍角公式，得到结论．
解答：解：∵z2+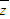
2=（cosθ+isinθ）2+（cosθ-isinθ）2
=2cos2θ=1
∴cos2θ=
，
∴sin2θ=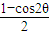
=
．
故选B
点评：抓住公式的结构特征对提高记忆公式的效率起到至关重要的作用，而且抓住了公式的结构特征，有利于在解题时观察分析题设和结论等三角函数式中所具有的相似性的结构特征，联想到相应的公式，从而找到解题的切入点．
解答：解：∵z2+
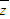2=（cosθ+isinθ）2+（cosθ-isinθ）2=2cos2θ=1
∴cos2θ=
，∴sin2θ=
=
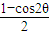
．故选B
点评：抓住公式的结构特征对提高记忆公式的效率起到至关重要的作用，而且抓住了公式的结构特征，有利于在解题时观察分析题设和结论等三角函数式中所具有的相似性的结构特征，联想到相应的公式，从而找到解题的切入点．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
若复数z=cosθ+isinθ且z2+
2=1，则sin2θ=（ ）
. |
| z |
A、
| ||
B、
| ||
C、
| ||
D、-
|