题目内容
若复数z=cosθ-isinθ所对应的点在第四象限，则θ所在的象限是（ ）
分析：根据所给的复数实部大于零、虚部小于零，求出角的正弦和余弦的符号，再由三角函数在各个象限的符号判断出此角所在的象限．
解答：解：∵z=cosθ-isinθ所对应的点在第四象限，
∴
，即
，
则角θ是第一象限角．
故选A．
∴
|
|
则角θ是第一象限角．
故选A．
点评：本题考查了复数与复平面内对应点之间的关系，以及象限角的定义和三角函数在各个象限中的符号．
练习册系列答案
阅读快车系列答案
相关题目
若复数z=cosθ+isinθ且z2+
2=1，则sin2θ=（ ）
. |
| z |
A、
| ||
B、
| ||
C、
| ||
D、-
|
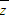2=1，则sin2θ=（ ）
