题目内容
已知f(x)=|x-a|.
(1)若a=1,作出f(x)的图象;
(2)当x∈[1,2],求f(x)的最小值;
(3)若g(x)=2x2+(x-a)|x-a|,求函数的最小值.
(1)若a=1,作出f(x)的图象;
(2)当x∈[1,2],求f(x)的最小值;
(3)若g(x)=2x2+(x-a)|x-a|,求函数的最小值.
分析:(1)当a=1时,f(x)=|x-1|,作出其图象即可;
(2)对a分a∈(-∞,1),a∈[1,2],a∈(2,+∞)三种情况讨论,再结合在相应区间上的单调性即可求得x∈[1,2]时f(x)的最小值;
(3)为了去掉绝对值符号,可分x≥a与x≤a两种情况讨论,再结合二次函数的性质即可求函数的最小值.
(2)对a分a∈(-∞,1),a∈[1,2],a∈(2,+∞)三种情况讨论,再结合在相应区间上的单调性即可求得x∈[1,2]时f(x)的最小值;
(3)为了去掉绝对值符号,可分x≥a与x≤a两种情况讨论,再结合二次函数的性质即可求函数的最小值.
解答: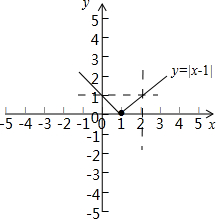 解:(1)因为a=1,作图如下(2分)
解:(1)因为a=1,作图如下(2分)
(2)①当a∈(-∞,1)时,f(x)=|x-a|=x-a,
因为f(x)在[1,2]递增,
所以f(x)min=f(1)=1-a;----------(4分)
②当a∈[1,2]时,当x=a时,f(x)min=0
③当a∈(2,+∞)时,f(x)=|x-a|=a-x,
因为f(x)在[1,2]递减,
所以f(x)min=f(2)=a-2----------(6分)
综上所述f(x)=
----------(8分)
(3)①当x≥a时,f(x)=3x2-2ax+a2=3(x-
)2+
a2,
∴若a≥0,f(x)在[a,+∞)上单调递增,f(x)min=f(a)=2a2;
若a<0,f(x)在[
,+∞)上单调递增,f(x)min=f(
)=
a2;
②当x≤a时,f(x)=x2+2ax-a2=(x+a)2-2a2,
若a≥0,f(x)在(-∞,-a]上单调递减[-a,a)上单调递增,f(x)min=f(-a)=-2a2;
若a<0,f(x)在(-∞,a]上单调递减,f(x)min=f(a)=2a2;
综上f(x)min=
----------(12分)
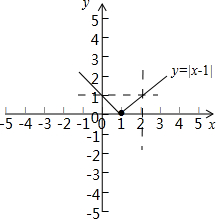 解:(1)因为a=1,作图如下(2分)
解:(1)因为a=1,作图如下(2分)(2)①当a∈(-∞,1)时,f(x)=|x-a|=x-a,
因为f(x)在[1,2]递增,
所以f(x)min=f(1)=1-a;----------(4分)
②当a∈[1,2]时,当x=a时,f(x)min=0
③当a∈(2,+∞)时,f(x)=|x-a|=a-x,
因为f(x)在[1,2]递减,
所以f(x)min=f(2)=a-2----------(6分)
综上所述f(x)=
|
(3)①当x≥a时,f(x)=3x2-2ax+a2=3(x-
| a |
| 3 |
| 2 |
| 3 |
∴若a≥0,f(x)在[a,+∞)上单调递增,f(x)min=f(a)=2a2;
若a<0,f(x)在[
| a |
| 3 |
| a |
| 3 |
| 2 |
| 3 |
②当x≤a时,f(x)=x2+2ax-a2=(x+a)2-2a2,
若a≥0,f(x)在(-∞,-a]上单调递减[-a,a)上单调递增,f(x)min=f(-a)=-2a2;
若a<0,f(x)在(-∞,a]上单调递减,f(x)min=f(a)=2a2;
综上f(x)min=
|
点评:本题考查带绝对值的函数,关键在于去掉函数式中的绝对值符号,方法是分类讨论,重点考查分类讨论思想与转化的思想,难点在于对含参数的二次函数的最值的研究,属于难题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由. ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由.