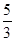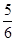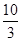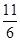题目内容
等差数列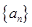 的公差
的公差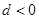 且
且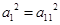 ,则数列
,则数列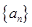 的前
的前 项和
项和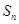 取得最大值时的项数
取得最大值时的项数 是( )
是( )
| A.5 | B.6 | C.5或6 | D.6或7 |
C
解析试题分析:因为数列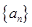 是等差数列,所以由
是等差数列,所以由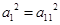 可得
可得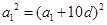 ,展开整理得
,展开整理得 ,因为
,因为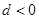 ,所以
,所以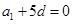
法一:由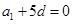 可得
可得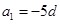 ,所以
,所以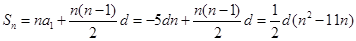
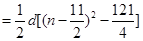 ,根据
,根据 ,结合二次函数的图像可知当
,结合二次函数的图像可知当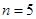 或
或 时,
时,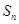 最大,选C;
最大,选C;
法二:由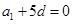 可得
可得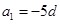 ,所以
,所以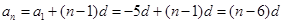 ,要使
,要使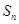 最大,则须满足
最大,则须满足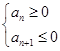 即
即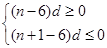 ,因为
,因为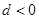 ,从中解得
,从中解得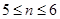 ,所以当
,所以当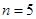 或
或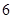 时,
时,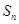 最大;
最大;
法三:由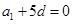 可得
可得 ,而
,而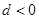 ,该等差数列
,该等差数列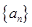 是单调递减数列,所以数列
是单调递减数列,所以数列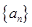 的前六项非负,所以当
的前六项非负,所以当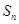 最大时,
最大时,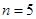 或
或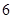 ,选C.
,选C.
考点:等差数列的通项公式及其前 项和.
项和.

练习册系列答案
相关题目
在等差数列 中,
中, =
= ,则数列
,则数列 的前11项和
的前11项和 =( ).
=( ).
| A.24 | B.48 | C.66 | D.132 |
已知等差数列 中,
中, , 则
, 则 的值是( )
的值是( )
| A.15 | B.30 | C.31 | D.64 |
已知等差数列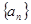 中,
中,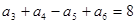 ,则
,则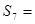 ( )
( )
| A.8 | B.21 | C.28 | D.35 |
设 是等差数列
是等差数列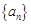 的前
的前 项和,若
项和,若 ,则
,则 ( )
( )
| A.1 | B.-1 | C.2 | D.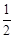 |
已知数列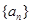 ,若点
,若点
 均在直线
均在直线 上,则数列
上,则数列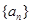 的前9项和
的前9项和 等于( )
等于( )
| A.18 | B.20 | C.22 | D.24 |
在等差数列{an}中,首项a1=120,公差d=-4,若Sn≤an(n≥2),则n的最小值为( )
| A.60 | B.62 | C.70 | D.72 |
设等差数列{an}的前n项和为Sn,已知(a4-1)3+2 013(a4-1)=1,(a2 010-1)3+2 013(a2 010-1)=-1,则下列结论中正确的是( )
| A.S2 013=2 013,a2 010<a4 |
| B.S2 013=2 013,a2 010>a4 |
| C.S2 013=2 012,a2 010≤a4 |
| D.S2 013=2 012,a2 010≥a4 |
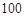 个面包分给
个面包分给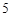 个人,使每人所得成等差数列,且使较大的三份之和的
个人,使每人所得成等差数列,且使较大的三份之和的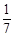 是较小的两份之和,则最小的
是较小的两份之和,则最小的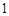 份为( )
份为( )